题目内容
15.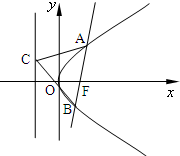 倾角为$\frac{π}{3}$的直线l过抛物线y2=4x的焦点F与抛物线交于A、B两点,点C是抛物线准线上的动点.
倾角为$\frac{π}{3}$的直线l过抛物线y2=4x的焦点F与抛物线交于A、B两点,点C是抛物线准线上的动点.(1)△ABC能否为正三角形?
(2)若△ABC是钝角三角形,求点C纵坐标的取值范围.
分析 (1)确定A,B的坐标,利用△ABC为正三角形,分类讨论,即可得出结论;
(2)若△ABC是钝角三角形,分类讨论,利用数量积运算,即可求点C纵坐标的取值范围.
解答  解:(1)直线l方程为y=$\sqrt{3}$(x-1),
解:(1)直线l方程为y=$\sqrt{3}$(x-1),
由y2=4x可得A(3,2$\sqrt{3}$),B($\frac{1}{3}$,-$\frac{2\sqrt{3}}{3}$)…(2分)
若△ABC为正三角形,则∠CAB=$\frac{π}{3}$,
由∠AFx=$\frac{π}{3}$,那么CA与x轴平行,此时|AC|=4…(4分)
又|AB|=3+$\frac{1}{3}$+2=$\frac{16}{3}$.
与|AC|=|AB|矛盾,所以△ABC不可能是正三角形…(6分)
(2)设C(-1,m),则$\overrightarrow{CA}$=(4,2$\sqrt{3}$-m),$\overrightarrow{CB}$=($\frac{4}{3}$,-$\frac{2\sqrt{3}}{3}$-m),
$\overrightarrow{CA}$•$\overrightarrow{CB}$=(m-$\frac{2\sqrt{3}}{3}$)2不可以为负,所以∠ACB不为钝角…(9分)
若∠CAB为钝角,则$\overrightarrow{AC}$•$\overrightarrow{AB}$<0,$\overrightarrow{BA}$=($\frac{8}{3}$,$\frac{8\sqrt{3}}{3}$),
则$\frac{32}{3}$+$\frac{8\sqrt{3}}{3}$(2$\sqrt{3}$-m)<0,得m>$\frac{10\sqrt{3}}{3}$…(11分)
若角∠ABC为钝角,则$\overrightarrow{BC}$•$\overrightarrow{BA}$<0且C、B、A不共线.
可得m<-$\frac{2\sqrt{3}}{3}$且m≠-6$\sqrt{3}$…(13分)
综上知,C点纵坐标的取值范围是m>$\frac{10\sqrt{3}}{3}$或m<-$\frac{2\sqrt{3}}{3}$且m≠-6$\sqrt{3}$…(14分)
点评 本题考查直线与抛物线的位置关系,考查向量知识的运用,考查分类讨论的数学思想,考查学生分析解决问题的能力,属于中档题.

 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案| A. | (xn)′=nxn-1(n∈N+) | B. | (ax)′=axlna | C. | (sinx)′=-cosx | D. | (lnx)′=$\frac{1}{x}$ |
| A. | 3 | B. | a | C. | -1 | D. | $\frac{2\sqrt{a}}{a-1}$ |
| A. | 0 | B. | 95% | C. | 90% | D. | 99.9% |