题目内容
12.对二次函数f(x)=ax2+bx+c(a为非零整数),四位同学分别给出下列结论,其中有且只有一个结论是错误的,则错误的结论是( )| A. | -1是f(x)的零点 | B. | 1是f(x)的极值点 | ||
| C. | 3是f(x)的极值 | D. | 点(2,8)在曲线y=f(x)上 |
分析 可采取排除法.分别考虑A,B,C,D中有一个错误,通过解方程求得a,判断是否为非零整数,即可得到结论.
解答 解:可采取排除法.
若A错,则B,C,D正确.即有f(x)=ax2+bx+c的导数为f′(x)=2ax+b,
即有f′(1)=0,即2a+b=0,①又f(1)=3,即a+b+c=3②,
又f(2)=8,即4a+2b+c=8,③由①②③解得,a=5,b=-10,c=8.符合a为非零整数.
若B错,则A,C,D正确,则有a-b+c=0,且4a+2b+c=8,且$\frac{4ac-{b}^{2}}{4a}$=3,解得a∈∅,不成立;
若C错,则A,B,D正确,则有a-b+c=0,且2a+b=0,且4a+2b+c=8,解得a=-$\frac{8}{3}$不为非零整数,不成立;
若D错,则A,B,C正确,则有a-b+c=0,且2a+b=0,且$\frac{4ac-{b}^{2}}{4a}$=3,解得a=-$\frac{3}{4}$不为非零整数,不成立.
故选:A.
点评 本题考查二次函数的极值、零点等概念,主要考查解方程的能力和判断分析的能力,属于中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
20.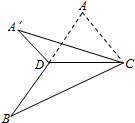 如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′-CD-B的平面角为α,则( )
如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′-CD-B的平面角为α,则( )
 如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′-CD-B的平面角为α,则( )
如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A′CD,所成二面角A′-CD-B的平面角为α,则( )| A. | ∠A′DB≤α | B. | ∠A′DB≥α | C. | ∠A′CB≤α | D. | ∠A′CB≥α |
 某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为l,如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和40千米,点N到l1,l2的距离分别为20千米和2.5千米,以l2,l1在的直线分别为x,y轴,建立平面直角坐标系xOy,假设曲线C符合函数y=$\frac{a}{{x}^{2}+b}$(其中a,b为常数)模型.
某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路,记两条相互垂直的公路为l1,l2,山区边界曲线为C,计划修建的公路为l,如图所示,M,N为C的两个端点,测得点M到l1,l2的距离分别为5千米和40千米,点N到l1,l2的距离分别为20千米和2.5千米,以l2,l1在的直线分别为x,y轴,建立平面直角坐标系xOy,假设曲线C符合函数y=$\frac{a}{{x}^{2}+b}$(其中a,b为常数)模型.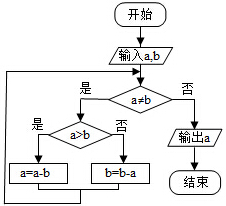 程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )
程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )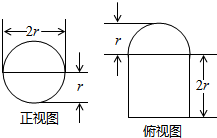 圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=( )
圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=( )