题目内容
2．在三棱住ABC-A1B1C1中，∠BAC=90°，其正视图和侧视图都是边长为1的正方形，俯视图是直角边长为1的等腰直角三角形，设M，N，P分别是AB，BC，B1C1的中点，则三棱锥P-A1MN的体积是$\frac{1}{24}$．分析 判断三视图对应的几何体的形状，画出图形，利用三视图的数据，求解三棱锥P-AMN的体积即可．
解答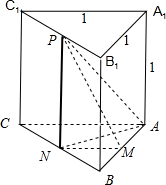 
解：由三视图可知，可知几何体的图形如图：几何体是底面为等腰直角三角形直角边长为1，高为1的直三棱柱，底面积为$\frac{1}{2}$，所求三棱锥的高为NP=1，三棱锥底面积是三棱柱底面三角形的$\frac{1}{4}$，
所求三棱锥P-A1MN的体积是：$\frac{1}{3}×\frac{1}{4}×\frac{1}{2}×1×1×1$=$\frac{1}{24}$．
故答案为：$\frac{1}{24}$．
点评 本题考查三视图与直观图的关系，组作出几何体的直观图是解题的关键之一，考查几何体的体积的求法，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
12．对二次函数f（x）=ax2+bx+c（a为非零整数），四位同学分别给出下列结论，其中有且只有一个结论是错误的，则错误的结论是（ ）
| A． | -1是f（x）的零点 | B． | 1是f（x）的极值点 | ||
| C． | 3是f（x）的极值 | D． | 点（2，8）在曲线y=f（x）上 |
如题图，椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点分别为F1，F2，过F2的直线交椭圆于P，Q两点，且PQ⊥PF1
10．随着我国经济的发展，居民的储蓄存款逐年增长．设某地区城乡居民人民币储蓄存款（年底余额）如下表：
（Ⅰ）求y关于t的回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$．
（Ⅱ）用所求回归方程预测该地区2015年（t=6）的人民币储蓄存款．
附：回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$中
$\left\{\begin{array}{l}{b=\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}=\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}}\\{a=\overline{y}-b\overline{t}}\end{array}\right.$．
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 时间代号t | 1 | 2 | 3 | 4 | 5 |
| 储蓄存款y（千亿元） | 5 | 6 | 7 | 8 | 10 |
（Ⅱ）用所求回归方程预测该地区2015年（t=6）的人民币储蓄存款．
附：回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$中
$\left\{\begin{array}{l}{b=\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}=\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{t}_{i}^{2}-n{\overline{t}}^{2}}}\\{a=\overline{y}-b\overline{t}}\end{array}\right.$．
17．设a，b为正实数，则“a＞b＞1”是“log2a＞log2b＞0”的（ ）
| A． | 充要条件 | B． | 充分不必要条件 | ||
| C． | 必要不充分条件 | D． | 既不充分也不必要条件 |
12．某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）在某一个周期内的图象时，列表并填入了部分数据，如表：
（1）请将上表数据补充完整，填写在相应位置，并直接写出函数f（x）的解析式；
（2）将y=f（x）图象上所有点向左平行移动θ（θ＞0）个单位长度，得到y=g（x）的图象．若y=g（x）图象的一个对称中心为（$\frac{5π}{12}$，0），求θ的最小值．
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{5π}{6}$ | |||
| Asin（ωx+φ） | 0 | 5 | -5 | 0 |
（2）将y=f（x）图象上所有点向左平行移动θ（θ＞0）个单位长度，得到y=g（x）的图象．若y=g（x）图象的一个对称中心为（$\frac{5π}{12}$，0），求θ的最小值．