题目内容
16．解关于x的不等式：$\frac{1-3x}{x-5}$≥-1．分析 根据分式不等式的解法建立不等式组即可得到结论
解答 解：$\frac{1-3x}{x-5}$≥-1，
∴$\frac{1-3x}{x-5}$+1≥0，
∴$\frac{-2x-4}{x-5}$≥0，
∴$\frac{x+2}{x-5}$≤0，
即（x+2）（x-5）≤0，且x-5≠0，
解得-2≤x＜5，
故不等式的解集为[-2，5）．
点评 本题主要考查不等式的解法，利用分式不等式的解法是解决本题的关键，注意分母不能取等号．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
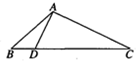如图，在△ABC中，已知点D在BC边上，AD⊥AC，sin∠BAC=$\frac{2\sqrt{2}}{3}$，AB=3$\sqrt{2}$，AD=3，求BD的长．