题目内容

函数y=9-ex，x∈[0，ln4]的最大值是
 
．
考点：函数的最值及其几何意义
专题：函数的性质及应用,导数的概念及应用
分析：求导数y′，可得y′＜0，则函数单调递减，可求x=0时取最大值．
解答： 解：∵y=9-ex，
∴y′=-ex＜0，
∴函数在[0，ln4]上单调递减，
∴当x=0时取得最大值f（0）=9-1=8．
故答案为；8．
点评：本题考察函数的最值求法，利用函数的单调性求解，属于基础题目．
练习册系列答案
相关题目
已知函数f（x）=x-alnx（a∈R）
（1）当a=2时，求曲线y=f（x）在点A（1，f（1））处的切线方程；
（2）讨论函数f（x）的单调性与极值；
（3）当a=2时，求函数f（x）在[1，3]上的最值．
已知元素为正整数的数集序列{1}，{2，3}，{4，5，6}，{7，8，9，10}，…从第二个数集开始，每一个数集比前一个数集多一个元素，且每一个数集中最小的元素比前一个数集中最大的元素大1，则第n个数集中所有元素之和Sn=
 
．
已知偶函数f（x）满足f（x+1）=f（x-1），且当x∈[0，1]时，f（x）=x2，则关于x的方程f（x）=2-2|x|
在[-5，5]上根的个数是（　　）
A、4个B、6个C、8个D、10个
已知函数f（x）=
ln(ax)
x+1
，曲线y=f（x）在x=1处的切线与直线x-2y=0平行．
（1）求a的值；
（2）若f（x）≤b-
2
x+1
恒成立，求实数b的最小值．
已知函数f（x）=
1
2
lnx+ax2（a∈R）．
（Ⅰ）若曲线y=f（x）在点(
1
2
，f(
1
2
))处的切线l切与直线l：x+2y-2=0垂直，求a的值；
（Ⅱ）讨论函数f（x）的单调性；若存在极值点x0∈（1，2），求实数a的取值范围．
若动点P（x，y）到定点A（3，4）的距离比P到x轴的距离多一个单位长度，则动点P的轨迹方程为
 
．
已知双曲线
x2
a2
-
y2
b2
=1的一条渐近线方程为y=
4
3
x，则双曲线的离心率为（　　）
A、
5
4
B、
5
3
C、
3
4
D、
3
2
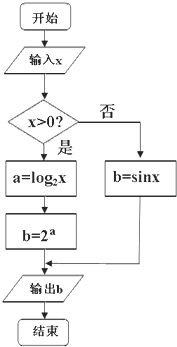如图所示的程序框图，若两次输入的x值分别是3π和-
π
3
，则两次运行程序输出的b值分别是（　　）
A、1，
3
2
B、0，
3
2
C、-π，-
3
2
D、3π，-
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网