题目内容

若动点P（x，y）到定点A（3，4）的距离比P到x轴的距离多一个单位长度，则动点P的轨迹方程为
 
．
考点：抛物线的标准方程
专题：圆锥曲线的定义、性质与方程
分析：由已知得
(x-3)2+(y-4)2
=|y|+1，由此能求出结果．
解答： 解：∵动点P（x，y）到定点A（3，4）的距离比P到x轴的距离多一个单位长度，
∴
(x-3)2+(y-4)2
=|y|+1，
整理，得x2-6x-10y+24=0或x2-6x-6y+24=0．
故答案为：x2-6x-10y+24=0或x2-6x-6y+24=0．
点评：本题考查点的轨迹方程的求法，是基础题，解题时要注意两点间距离公式的合理运用．
练习册系列答案
相关题目
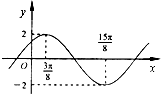已知函数f（x）=2sin（ωx+ϕ）（ω＞0，0＜ϕ＜π）的图象如图所示，则ω等于（　　）
A、
1
3
B、
2
3
C、1
D、2
坐标平面上的点（x，y）位于线性约束条件
x+y≤5
y≤x+1
x≥0
y≥0
所表示的区域内（含边界），则目标函数z=3x+4y的最大值是
 
．
函数y=9-ex，x∈[0，ln4]的最大值是
 
．
已知曲线C的极坐标方程为ρ=
4cosθ
sin2θ
，以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系，直线l的参数方程为
x=-
2
2
t
y=1+
2
2
t
（t为参数）．
（Ⅰ）把曲线C的极坐标方程化为直角坐标方程，把直线l的参数方程化为普通方程；
（Ⅱ）求直线l被曲线C截得的线段AB的长．
已知实数x，y满足约束条件
y≥1
y≤2x-1
x+y≤5
，则目标函数z=x-y的最小值等于
 
．
在平面直角坐标系中，不等式组
x+y≥0
x-y+4≥0
x≤a
，（a是常数）表示的平面区域面积是9，那么实数a的值为（　　）
A、3
2
+2
B、-3
2
+2
C、-5
D、1
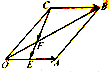如图，在平行四边形OABC中，E是OA的中点，F在对角线OB上，且OF=
1
3
OB，记
OA
=
a
，
OC
=
b
．
（1）试用
a
，
b
表示
CE
，
CF
；
（2）证明：C，E，F三点共线．
下列函数中，函数y=（
1
2
）x的反函数是（　　）
A、y=x 
1
2
B、y=2x
C、f（x）=log2x
D、y=log 
1
2
x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网