题目内容
已知函数f(x)=
,曲线y=f(x)在x=1处的切线与直线x-2y=0平行.
(1)求a的值;
(2)若f(x)≤b-
恒成立,求实数b的最小值.
| ln(ax) |
| x+1 |
(1)求a的值;
(2)若f(x)≤b-
| 2 |
| x+1 |
考点:利用导数研究曲线上某点切线方程
专题:综合题,导数的概念及应用
分析:(1)求出原函数的导函数,得到函数在x=1处的导数,由导数值等于
,求得实数a的值;
(2)由题得:b≥
(x>0)恒成立,构造g(x)=
,求出g(x)max=1,即可求实数b的最小值.
| 1 |
| 2 |
(2)由题得:b≥
| 2+lnx |
| x+1 |
| 2+lnx |
| x+1 |
解答:
解:(1)f'(x)=
=
,
由f'(1)=
=
,解得a=1.
(2)∵a=1,∴f(x)=
,∴由题得:b≥
(x>0)恒成立,
设g(x)=
,则g'(x)=
,再设h(x)=
,则h'(x)=-
<0,
∴h(x)在(0,+∞)上递减,
又h(1)=0,
∴当x∈(0,1)时,h(x)>0,即g'(x)>0,∴g(x)在(0,1)上为增函数;
当x∈(1,+∞)时,h(x)<0,即g'(x)<0,∴g(x)在(1,+∞)上为减函数;
∴g(x)max=g(1)=1,
∴只需b≥g(x)max=1,即b≥1,
∴b的最小值bmin=1.
| ||
| (x+1)2 |
1+
| ||
| (x+1)2 |
由f'(1)=
| 2-lna |
| 4 |
| 1 |
| 2 |
(2)∵a=1,∴f(x)=
| lnx |
| x+1 |
| 2+lnx |
| x+1 |
设g(x)=
| 2+lnx |
| x+1 |
| ||
| (x+1)2 |
| ||
| (x+1)2 |
| x+1 |
| x2 |
∴h(x)在(0,+∞)上递减,
又h(1)=0,
∴当x∈(0,1)时,h(x)>0,即g'(x)>0,∴g(x)在(0,1)上为增函数;
当x∈(1,+∞)时,h(x)<0,即g'(x)<0,∴g(x)在(1,+∞)上为减函数;
∴g(x)max=g(1)=1,
∴只需b≥g(x)max=1,即b≥1,
∴b的最小值bmin=1.
点评:本题考查了利用导数研究函数在某点处的切线方程,考查函数的最值,正确分离参数是关键,是中档题.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
已知数列{an}满足:a1=-
,an+1=1-
,则a2009=( )
| 1 |
| 4 |
| 1 |
| an |
A、
| ||
| B、5 | ||
C、-
| ||
D、
|
在平面直角坐标系中,不等式组
,(a是常数)表示的平面区域面积是9,那么实数a的值为( )
|
A、3
| ||
B、-3
| ||
| C、-5 | ||
| D、1 |
 已知等差数列{an}的公差为d,前n项和为Sn,且满足
已知等差数列{an}的公差为d,前n项和为Sn,且满足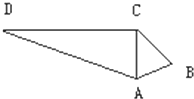 如图在四边形ABCD中,AC⊥DC,△ADC的面积为30cm2,DC=12cm,AB=3cm,BC=4cm求△ABC的面积.
如图在四边形ABCD中,AC⊥DC,△ADC的面积为30cm2,DC=12cm,AB=3cm,BC=4cm求△ABC的面积.