题目内容
【题目】已知数列{an}的前n项和为Sn ， 满足 
，且a1=3．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求证： 
．
【答案】解：（Ⅰ）数列{an}的前n项和为Sn ， 且 
， ∴Sn﹣Sn﹣1=2an﹣1+1，（n≥2，n∈N*），
即an=2an﹣1+1（n≥2，n∈N*），
∴an+1=2（an﹣1+1），
∴数列{an+1}是等比数列；
又a1+1=3+1=4，
∴ 
，
∴ 
；
（Ⅱ）由（Ⅰ）知， 
，
∴{ 
}是首项为 
，公比为 
的等比数列，
因此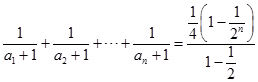 
= 
【解析】（Ⅰ）由数列{an}的前n项和与通项公式的定义，得出an=2an﹣1+1（n≥2，n∈N*），从而得出数列{an+1}是等比数列，由此求出{an}的通项公式； （Ⅱ）由（Ⅰ）写出数列{an+1}的通项公式，从而得出{ 
}是等比数列，求出其前n项和，即可证明不等式成立．
练习册系列答案
相关题目
【题目】把单位正方体的六个面分别染上6种颜色，并画上个数不同的金鸡，各面的颜色与鸡的个数对应如表：
面上所染颜色 | 红 | 黄 | 蓝 | 青 | 紫 | 绿 |
该面上的金鸡个数 | 1 | 2 | 3 | 4 | 5 | 6 |
取同样的4个上述的单位正方体拼成一个如图所示的水平放置的长方体.则这个长方体的下底面总计画有______个金鸡
