题目内容
【题目】已知函数f（x）＝xlnx，
（1）求函数f（x）过（﹣1，﹣2）的切线的方程
（2）过点P（1，t）存在两条直线与曲线y＝f（x）相切，求t的取值范围
【答案】（1）y＝x﹣1（2）（﹣∞，0）
【解析】
（1）求导得到f′（x）＝1+lnx，设切点为（m，n），利用切线方程公式计算得到答案.
（2）导数为f′（x）＝1+lnx，设切点为（u，v）化简得到t﹣1＝lnu﹣u在（0，+∞）有两解，求函数的最值得到答案.
（1）函数f（x）＝xlnx的导数为f′（x）＝1+lnx，
设切点为（m，n），可得切线的斜率为1+lnm，切线方程为y﹣mlnm＝（1+lnm）（x﹣m），
代入（﹣1，﹣2），可得﹣2﹣mlnm＝（1+lnm）（﹣1﹣m），
化为m+lnm＝1，由y＝x+lnx在（0，+∞）递增，且x＝1时，y＝1，
可得m+lnm＝1的解为m＝1，
则所求切线的方程为y＝x﹣1；
（2）函数f（x）＝xlnx的导数为f′（x）＝1+lnx，
设切点为（u，v），则切线的斜率为f′（u）＝1+lnu，
即有切线的方程为y﹣ulnu＝（1+lnu）（x﹣u），
代入点P（1，t），即有t﹣ulnu＝（1+lnu）（1﹣u），
即为t﹣1＝lnu﹣u在（0，+∞）有两解，
由g（x）＝lnx﹣x的导数为g′（x）
1，
可得x＞1，g（x）递减，0＜x＜1，g（x）递增．
可得x＝1，取得最大值g（1）＝﹣1，即有t﹣1＜﹣1，解得t＜0．
故实数t的取值范围时（﹣∞，0）．
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店，为合理安排各地区加盟店的个数，先在其中5个地区试点，得到试点地区加盟店个数分别为1，2，3，4，5时，单店日平均营业额
（万元）的数据如下：
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
（1）求单店日平均营业额（万元）与所在地区加盟店个数
（个）的线性回归方程；
（2）根据试点调研结果，为保证规模和效益，在其他5个地区，该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元，求一个地区开设加盟店个数
的所有可能取值；
（3）小赵与小王都准备加入该公司的加盟店，根据公司规定，他们只能分别从其他五个地区（加盟店都不少于2个）中随机选一个地区加入，求他们选取的地区相同的概率.
（参考数据及公式：
，
，线性回归方程
，其中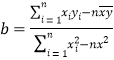
，
.）
