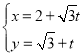题目内容
【题目】若定义在R上的函数![]() ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数![]() 使得
使得![]() 对任意实数x都成立,则称
对任意实数x都成立,则称![]() 是一个“k~特征函数”.则下列结论中正确命题序号为____________.
是一个“k~特征函数”.则下列结论中正确命题序号为____________.
①![]() 是一个“k~特征函数”;②
是一个“k~特征函数”;②![]() 不是“k~特征函数”;
不是“k~特征函数”;
③![]() 是常数函数中唯一的“k~特征函数”;④“
是常数函数中唯一的“k~特征函数”;④“![]() ~特征函数”至少有一个零点;
~特征函数”至少有一个零点;
【答案】①②④
【解析】
根据题意:依次检验定义域,连续性,是否存在常数![]() 使得
使得![]() 对任意实数x都成立即可.
对任意实数x都成立即可.
①![]() ,考虑
,考虑![]() 即:
即:![]() ,
,![]() ,
,
考虑![]() ,必存在
,必存在![]() 使
使![]() ,
,
即存在![]() ,使得
,使得![]() 对任意实数x都成立,所以①正确;
对任意实数x都成立,所以①正确;
②![]() ,讨论
,讨论![]() ,即
,即![]()
当![]() 时,关于
时,关于![]() 的方程
的方程![]() 无解,
无解,
不存在![]() 使
使![]() 对任意实数x都成立,
对任意实数x都成立,
所以![]() 不是“k~特征函数”,所以②正确;
不是“k~特征函数”,所以②正确;
③设常数函数![]() ,讨论
,讨论![]() ,即
,即![]() ,
,
当![]() 时对任意实数x都成立,所以任何一个常数函数都可以是“-1~特征函数”,
时对任意实数x都成立,所以任何一个常数函数都可以是“-1~特征函数”,
所以③错误;
④设![]() 是“
是“![]() ~特征函数”, 则
~特征函数”, 则![]() 是定义在R上的连续函数,
是定义在R上的连续函数,
且![]() 对任意实数x都成立,
对任意实数x都成立,
下面利用反证法证明![]() 必有零点:
必有零点:
证明:假设![]() 没有零点,因为
没有零点,因为![]() 是定义在R上的连续函数,则
是定义在R上的连续函数,则![]() 恒成立,或
恒成立,或![]() 恒成立;
恒成立;
当![]() 恒成立,则
恒成立,则![]() ,
,![]() ,与题矛盾;
,与题矛盾;
当![]() 恒成立,则
恒成立,则![]() ,
,![]() ,与题矛盾;
,与题矛盾;
所以![]() 必有零点,所以④正确.
必有零点,所以④正确.
故答案为:①②④

练习册系列答案
相关题目