题目内容
10．已知函数f（x）为奇函数，且当x≥0时，f（x）=$\frac{1}{{3}^{x}+2013}$-a，则f（log3$\frac{1}{2}$）=-$\frac{4029}{4058210}$．分析 根据奇函数的结论f（0）=0求出a，再由对数的运算
解答 解：∵函数f（x）为奇函数，∴f（0）=$\frac{1}{2014}$-a=0，
解得a=$\frac{1}{2014}$．
f（log3$\frac{1}{2}$）=-f（log32）-$\frac{1}{2014}$=-$\frac{1}{2015}$-$\frac{1}{2014}$=-$\frac{4029}{4058210}$．
故答案为：-$\frac{4029}{4058210}$．
点评 本题考查了对数的运算，以及奇函数的结论、关系式得应用，属于基础题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
1．已知tanα=2（α∈（0，π）），则cos（$\frac{5π}{2}$+2α）=（ ）
| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | -$\frac{3}{5}$ | D． | -$\frac{4}{5}$ |
18．已知函数f（n）=$\left\{\begin{array}{l}{0，x=1}\\{f（n-1）+3，（n∈{N^*}，n≥2）}\end{array}$，则f（3）等于（ ）
| A． | 0 | B． | 3 | C． | 6 | D． | 9 |
2．若关于x的不等式x2+ax-c＜0的解集为{x|-2＜x＜1}，则函数g（x）=eax•x2的单调递减区间为（ ）
| A． | （-∞，0） | B． | （-∞，-2） | C． | （-2，-1） | D． | （-2，0） |
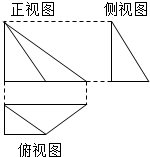
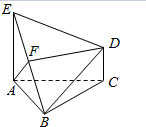如图，△ABC为正三角形，AE和CD都垂直于平而ABC，F是BE中点，AE=AB=2，CD=1．