题目内容
12.已知函数f(x)=x2-2x,若函数F(x)=|f(x)|+|f(a-x)|-t有四个零点,且它们的和为2,则实数t的取值范围是(1,$\frac{3}{2}$).分析 函数y=|f(x)|的图象与函数y=|f(a-x)|的图象关于直线x=$\frac{a}{2}$对称,故函数F(x)=|f(x)|+|f(a-x)|-t的图象关于直线x=$\frac{a}{2}$对称,进而可得a值,进而将函数g(x)=|f(x)|+|f(a-x)|的解析式化为分类函数的形式,并画出函数的图象,数形结合,可得答案.
解答 解:函数y=|f(x)|的图象与函数y=|f(a-x)|的图象关于直线x=$\frac{a}{2}$对称,
故函数F(x)=|f(x)|+|f(a-x)|-t的图象关于直线x=$\frac{a}{2}$对称,
若函数F(x)=|f(x)|+|f(a-x)|-t有四个零点,且它们的和为2,
则a=1,
令g(x)=|f(x)|+|f(a-x)|=|x2-2x|+|(1-x)2-2(1-x)|=|x2-2x|+|x2-1|=$\left\{\begin{array}{l}2{x}^{2}-2x-1,x<-1\\-2x+1,-1≤x≤0\\-2{x}^{2}+2x+1,0<x<1\\ 2x-1,1≤x≤2\\ 2{x}^{2}-2x-1,x>2\end{array}\right.$,
其图象如下图所示: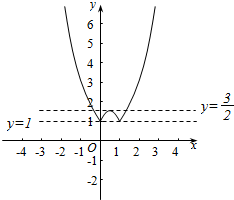
由图可得:实数t∈(1,$\frac{3}{2}$)时,g(x)=|f(x)|+|f(a-x)|与y=t有四个交点,
故函数F(x)=|f(x)|+|f(a-x)|-t有四个零点,
故答案为:(1,$\frac{3}{2}$)
点评 本题考查的知识点是函数零点的判定定理,函数图象,分段函数的应用,分类讨论思想,数形结合思想,难度中档.

练习册系列答案
相关题目
2.若关于x的不等式x2+ax-c<0的解集为{x|-2<x<1},则函数g(x)=eax•x2的单调递减区间为( )
| A. | (-∞,0) | B. | (-∞,-2) | C. | (-2,-1) | D. | (-2,0) |
4.下列条件中可以确定两条直线平行的是( )
| A. | 垂直同一条直线的两条直线 | B. | 平行同一平面的两条直线 | ||
| C. | 平行同一条直线的两条直线 | D. | 和同一平面所成角相等 |
2.已知θ是三角形的-个内角,且sin($\frac{π}{2}$-θ)=$\frac{\sqrt{2}}{2}$,则角θ等于( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{4}$或$\frac{3π}{4}$ | D. | $\frac{π}{3}$ |
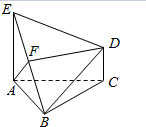 如图,△ABC为正三角形,AE和CD都垂直于平而ABC,F是BE中点,AE=AB=2,CD=1.
如图,△ABC为正三角形,AE和CD都垂直于平而ABC,F是BE中点,AE=AB=2,CD=1.