题目内容
14．若f（x+π）=f（x），且f（-x）=f（x），则f（x）可以是（ ）| A． | sin2x | B． | cosx | C． | cos|x| | D． | |sinx| |
分析 根据已知分析函数的周期性和奇偶性，利用排除法可得答案．
解答 解：若f（x+π）=f（x），则函数的周期为π，固排除B，C；
若f（-x）=f（x）则函数为偶函数，固排除A，
故选：D．
点评 本题考查的知识点是函数的周期性和函数的奇偶性，熟练掌握三角函数的图象和性质，是解答的关键．
练习册系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
5．下列函数中，随x的增大，增长速度最快的是（ ）
| A． | y=2x | B． | y=10000x | C． | y=log3x | D． | y=x3 |
9．函数y=${log}_{\frac{3}{2}}$（x2-3x-4）的单调增区间为（ ）
| A． | （-∞，-1） | B． | （4，+∞） | C． | （-∞，$\frac{3}{2}$） | D． | （$\frac{3}{2}$，+∞） |
19．若（1-2i）i=a+bi（a，b∈R，i为虚数单位），则ab=（ ）
| A． | -2 | B． | 2 | C． | 3 | D． | 1 |
8．
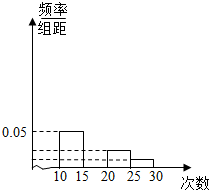对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图：
（1）求出表中M、p、m、n的值；
（2）补全频率分布直方图；若该校高一学生有360人，估计他们参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间[20，25）内的概率．
对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图：| 分组 | 频数 | 频率 |
| [10，15） | 10 | 0.25 |
| [15，20） | 25 | n |
| [20，25） | m | p |
| [25，30） | 2 | 0.05 |
| 合计 | M | 1 |
（2）补全频率分布直方图；若该校高一学生有360人，估计他们参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间[20，25）内的概率．