题目内容
7.函数f(x)=x cos2x在区间[0,2π]上的零点的个数为5.分析 令f(x)=0,可得x=0或cos2x=0,cos2x=0,可得2x=kπ+$\frac{π}{2}$,k∈Z,由k的取值,即可得到所求零点的个数.
解答 解:令f(x)=0,可得
x=0或cos2x=0,
若cos2x=0,可得2x=kπ+$\frac{π}{2}$,k∈Z,
即x=$\frac{kπ}{2}$+$\frac{π}{4}$,k∈Z,
即有k=0,x=$\frac{π}{4}$;k=1,x=$\frac{3π}{4}$;k=2,x=$\frac{5π}{4}$;
k=3,x=$\frac{7π}{4}$.
综上可得,f(x)在区间[0,2π]上的零点的个数为5.
故答案为:5.
点评 本题考查函数的零点的求法,注意运用三角函数的周期,考查运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若f(x+π)=f(x),且f(-x)=f(x),则f(x)可以是( )
| A. | sin2x | B. | cosx | C. | cos|x| | D. | |sinx| |
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,一条准线方程为x=2.过椭圆的上顶点A作一条与x轴、y轴都不垂直的直线交椭圆于另一点P,P关于x轴的对称点为Q.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,一条准线方程为x=2.过椭圆的上顶点A作一条与x轴、y轴都不垂直的直线交椭圆于另一点P,P关于x轴的对称点为Q.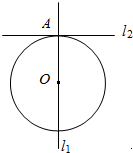 如图,已知l1⊥l2,圆心在l1上,半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=$si{n^2}\frac{x}{2}$,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )
如图,已知l1⊥l2,圆心在l1上,半径为1m的圆O在t=0时与l2相切于点A,圆O沿l1以1m/s的速度匀速向上移动,圆被直线l2所截上方圆弧长记为x,令y=$si{n^2}\frac{x}{2}$,则y与时间t(0≤t≤1,单位:s)的函数y=f(t)的图象大致为( )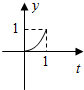
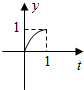
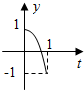

 已知函数f(x)=x2+2x|x-a|,其中a∈R.
已知函数f(x)=x2+2x|x-a|,其中a∈R.