题目内容
【题目】在平面直角坐标系xOy中,已知圆C经过点A(1,3) ,B(4,2),且圆心在直线l:x-y-1=0上.
(1)求圆C的方程;
(2)设P是圆D:x2+y2+8x-2y+16=0上任意一点,过点P作圆C的两条切线PM,PN,M,N为切点,试求四边形PMCN面积S的最小值及对应的点P坐标.
【答案】(1) x2+y2-4x-2y=0 (2) S最小10,P(-3,1)
【解析】试题分析:(1)设圆C的方程为x2+y2+Dx+Ey+F=0,根据条件得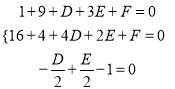 ,即可得解;
,即可得解;
(2)依题意,S=2S△PMC=PM×MC =![]() ,当PC最小时,S最小,求PC最小即可.
,当PC最小时,S最小,求PC最小即可.
试题解析:
(1)设圆C的方程为x2+y2+Dx+Ey+F=0,其圆心为(-![]() ,-
,-![]() ).
).
因为圆C经过点A(1,3) ,B(4,2),且圆心在直线l:x-y-1=0上,
所以
解得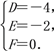
所求圆C的方程为x2+y2-4x-2y=0.
(2)由(1)知,圆C的方程为(x-2)2+(y-1)2=5.
依题意,S=2S△PMC=PM×MC =![]() ×
×![]() .
.
所以当PC最小时,S最小.
因为圆M:x2+y2+8x-2y+16=0,所以M(-4,1),半径为1.
因为C(2,1),所以两个圆的圆心距MC=6.
因为点P∈M,且圆M的半径为1,
所以PCmin=6-1=5.
所以Smin=![]() ×
×![]() =10.
=10.
此时直线MC:y=1,从而P(-3,1).

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】已知圆![]() 的圆心在直线
的圆心在直线![]() 上,且圆
上,且圆![]() 经过点
经过点![]() 与点
与点![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线,求切线所在的直线的方程.
的切线,求切线所在的直线的方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)求出线段![]() 的中点
的中点![]() ,进而得到线段
,进而得到线段![]() 的垂直平分线为
的垂直平分线为![]() ,与
,与![]() 联立得交点
联立得交点![]() ,∴
,∴![]() .则圆
.则圆![]() 的方程可求
的方程可求
(2)当切线斜率不存在时,可知切线方程为![]() .
.
当切线斜率存在时,设切线方程为![]() ,由
,由![]() 到此直线的距离为
到此直线的距离为![]() ,解得
,解得![]() ,即可到切线所在直线的方程.
,即可到切线所在直线的方程.
试题解析:((1)设 线段![]() 的中点为
的中点为![]() ,∵
,∵![]() ,
,
∴线段![]() 的垂直平分线为
的垂直平分线为![]() ,与
,与![]() 联立得交点
联立得交点![]() ,
,
∴![]() .
.
∴圆![]() 的方程为
的方程为![]() .
.
(2)当切线斜率不存在时,切线方程为![]() .
.
当切线斜率存在时,设切线方程为![]() ,即
,即![]() ,
,
则![]() 到此直线的距离为
到此直线的距离为![]() ,解得
,解得![]() ,∴切线方程为
,∴切线方程为![]() .
.
故满足条件的切线方程为![]() 或
或![]() .
.
【点睛】本题考查圆的方程的求法,圆的切线,中点弦等问题,解题的关键是利用圆的特性,利用点到直线的距离公式求解.
【题型】解答题
【结束】
20
【题目】某小型企业甲产品生产的投入成本![]() (单位:万元)与产品销售收入
(单位:万元)与产品销售收入![]() (单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
(单位:万元)存在较好的线性关系,下表记录了最近5次产品的相关数据.
| 7 | 10 | 11 | 15 | 17 |
| 19 | 22 | 25 | 30 | 34 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据(1)中的回归方程,判断该企业甲产品投入成本20万元的毛利率更大还是投入成本24万元的毛利率更大(![]() )?
)?
相关公式: 
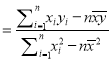 ,
, ![]() .
.
【题目】某中学对男女学生是否喜爱古典音乐进行了一个调查,调查者对学校高三年级随机抽取了100名学生,调查结果如表:
喜爱 | 不喜爱 | 总计 | |
男学生 | 60 | 80 | |
女学生 | |||
总计 | 70 | 30 |
附:K2= ![]()
P(K2≥k0) | 0.100 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
(1)完成如表,并根据表中数据,判断是否有95%的把握认为“男学生和女学生喜欢古典音乐的程度有差异”;
(2)从以上被调查的学生中以性别为依据采用分层抽样的方式抽取10名学生,再从这10名学生中随机抽取5名学生去某古典音乐会的现场观看演出,求正好有X个男生去观看演出的分布列及期望.
