题目内容
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )已知双曲线
)已知双曲线![]() 的离心率是椭圆
的离心率是椭圆![]() 的离心率的倒数,其顶点为椭圆的焦点,求双曲线
的离心率的倒数,其顶点为椭圆的焦点,求双曲线![]() 的方程.
的方程.
(![]() )设直线
)设直线![]() 与双曲线交于
与双曲线交于![]() ,
, ![]() 两点,过
两点,过![]() 的直线
的直线![]() 与线段
与线段![]() 有公共点,求直线
有公共点,求直线![]() 的倾斜角的取值范围.
的倾斜角的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(![]() )利用点在椭圆上、离心率进行求解;(
)利用点在椭圆上、离心率进行求解;(![]() )先利用双曲线和椭圆的关系求出有关几何量,再写出双曲线的方程即可;(
)先利用双曲线和椭圆的关系求出有关几何量,再写出双曲线的方程即可;(![]() )先联立直线和双曲线的方程求出点
)先联立直线和双曲线的方程求出点![]() ,
, ![]() 的坐标,再利用斜率公式求边界直线的斜率,进而确定直线
的坐标,再利用斜率公式求边界直线的斜率,进而确定直线![]() 的斜率和倾斜角的取值范围.
的斜率和倾斜角的取值范围.
试题解析:(![]() )由题意可得
)由题意可得![]() ,
, ![]() ,
,
解得![]() ,
, ![]() ,
,
故椭圆方程为![]() .
.
(![]() )由题意可得双曲线离心率
)由题意可得双曲线离心率![]() ,
,
![]() ,则
,则![]() ,
, ![]() ,
,
故双曲线方程为![]() .
.
(![]() )联立
)联立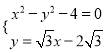 ,得
,得![]() ,
,
解得![]() 或
或![]() ,则
,则![]() ,
, ![]() .
.
则![]() ,则
,则 ,
,
即直线![]() 的倾斜角的取值范围为
的倾斜角的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由 ![]() 算得,
算得, ![]() .
.
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”