题目内容
【题目】试分别用综合法、分析法、反证法等三种方法，证明下列结论：已知0＜a＜1，则 
+ 
≥9．
【答案】证明：分析法： 
+ 
≥9 
≥9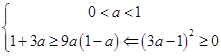 
反证法：假设 + ＜9，通分得 ＜9．
∵0＜a＜1，∴1+3a＜9a（1﹣a），整理得（3a﹣1）2＜0，这与平方数不小于0矛盾．
∴假设不成立，则 + ≥9．
综合法：由（3a﹣1）2≥0，变形得1+3a≥9a（1﹣a）．
∵0＜a＜1，∴ ≥9，即 + ≥9．
【解析】分析法是从结论出发找出要证结论的充分条件；反证法是假设结论不成立，从假设出发：同分；两边同时乘以a（1﹣a）；得到不成立的结论，从而得证；综合法即将分析法的每一步倒过来．
【考点精析】解答此题的关键在于理解反证法的相关知识，掌握从命题结论的反面出发（假设），引出(与已知、公理、定理…)矛盾，从而否定假设证明原命题成立，这样的证明方法叫做反证法．
练习册系列答案
相关题目
