Question

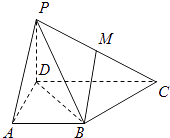
【题目】如图，已知二面角α﹣MN﹣β的大小为60°，菱形ABCD在面β内，A、B两点在棱MN上，∠BAD=60°，E是AB的中点，DO⊥面α，垂足为O．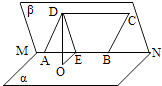

（1）证明：AB⊥平面ODE；
（2）求异面直线BC与OD所成角的余弦值．

Answer 1

【答案】
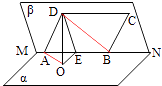
（1）证明：如图

∵DO⊥面α，ABα，∴DO⊥AB，

连接BD，由题设知，△ABD是正三角形，

又E是AB的中点，∴DE⊥AB，又DO∩DE=D，

∴AB⊥平面ODE；

（2）解：∵BC∥AD，

∴BC与OD所成的角等于AD与OD所成的角，即∠ADO是BC与OD所成的角，

由（1）知，AB⊥平面ODE，

∴AB⊥OE，又DE⊥AB，于是∠DEO是二面角α﹣MN﹣β的平面角，

从而∠DEO=60°，不妨设AB=2，则AD=2，易知DE= ，

在Rt△DOE中，DO=DEsin60°= ，连AO，在Rt△AOD中，cos∠ADO= = ，

故异面直线BC与OD所成角的余弦值为 ．

【解析】（1）运用直线与平面垂直的判定定理，即可证得，注意平面内的相交二直线；（2）根据异面直线的定义，找出所成的角为∠ADO，说明∠DEO是二面角α﹣MN﹣β的平面角，不妨设AB=2，从而求出OD的长，再在直角三角形AOD中，求出cos∠ADO．
【考点精析】解答此题的关键在于理解异面直线及其所成的角的相关知识，掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系，以及对直线与平面垂直的判定的理解，了解一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．