题目内容
已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)<f(x),且f(x+2)为偶函数,f(4)=1,则不等式f(x)<ex的解集为( )
| A.(-2,+∞) | B.(0,+∞) |
| C.(1,+∞) | D.(4,+∞) |
B
因为f(x+2)为偶函数,
所以f(2-x)=f(x+2),因此f(0)=f(4)=1.
令h(x)=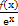 ,则原不等式即为h(x)<h(0).
,则原不等式即为h(x)<h(0).
又h'(x)=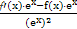 =
=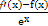 ,
,
依题意f'(x)<f(x),故h'(x)<0,因此函数h(x)在R上是减函数,所以由h(x)<h(0)得x>0.
所以f(2-x)=f(x+2),因此f(0)=f(4)=1.
令h(x)=
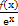 ,则原不等式即为h(x)<h(0).
,则原不等式即为h(x)<h(0).又h'(x)=
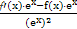 =
=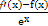 ,
,依题意f'(x)<f(x),故h'(x)<0,因此函数h(x)在R上是减函数,所以由h(x)<h(0)得x>0.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
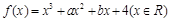 在
在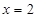 处取得极小值.
处取得极小值.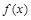 的极小值是
的极小值是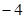 ,求
,求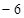 ,问:是否存在实数
,问:是否存在实数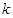 ,使得函数
,使得函数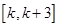 上单调递减?若存在,求出
上单调递减?若存在,求出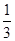 x3-
x3-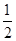 x2+bx的图象在交点(0,0)处有公共切线.
x2+bx的图象在交点(0,0)处有公共切线.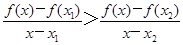 .
.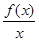 >0,若a=
>0,若a=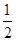 f
f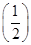 ,b=-2f(-2),c=ln
,b=-2f(-2),c=ln 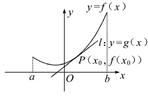
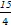 x-9都相切,则a等于( )
x-9都相切,则a等于( )
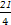
 或-
或-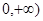 上的非负可导函数f(x)满足xf′(x)
上的非负可导函数f(x)满足xf′(x)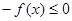 ,对任意正数
,对任意正数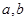 ,若满足
,若满足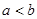 ,则必有( )
,则必有( )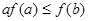
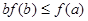
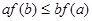
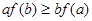
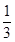 x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.
x3+ax2-bx(a,b∈R),若y=f(x)在区间[-1,2]上是单调减函数,则a+b的最小值为______.