题目内容
已知a,b∈R,函数f(x)=a+ln(x+1)的图象与g(x)=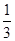 x3-
x3-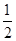 x2+bx的图象在交点(0,0)处有公共切线.
x2+bx的图象在交点(0,0)处有公共切线.
(1)证明:不等式f(x)≤g(x)对一切x∈(-1,+∞)恒成立;
(2)设-1<x1<x2,当x∈(x1,x2)时,证明: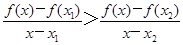 .
.
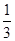 x3-
x3-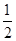 x2+bx的图象在交点(0,0)处有公共切线.
x2+bx的图象在交点(0,0)处有公共切线.(1)证明:不等式f(x)≤g(x)对一切x∈(-1,+∞)恒成立;
(2)设-1<x1<x2,当x∈(x1,x2)时,证明:
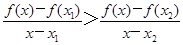 .
.(1)见解析(2)见解析
(1)由题意得f′(x)=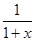 ,g′(x)=x2-x+b,x>-1,
,g′(x)=x2-x+b,x>-1,
则 解得
解得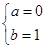
∴f(x)=ln(x+1)(x>-1),g(x)=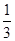 x3-
x3-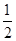 x2+x.
x2+x.
令h(x)=f(x)-g(x)
=ln(x+1)-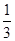 x3+
x3+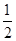 x2-x(x>-1),
x2-x(x>-1),
∴h′(x)=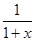 -x2+x-1=-
-x2+x-1=-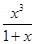 ,
,
∴h(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
∴h(x)≤h(0)=0,∴f(x)≤g(x).
(2)当x∈(x1,x2)时,由题意得-1<x1<x<x2,
①设u(x)=(x+1)[f(x)-f(x1)]-(x-x1),
则u′(x)=ln(x+1)-ln(x1+1)>0,
∴u(x)>u(x1)=0,即(x+1)[f(x)-f(x1)]-(x-x1)>0,
∴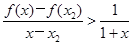 ;
;
②设v(x)=(x+1)[f(x)-f(x2)]-(x-x2),
则v′(x)=ln(x+1)-ln(x2+1)<0,
∴v(x)>v(x2)=0,即(x+1)[f(x)-f(x2)]-(x-x2)>0,
∴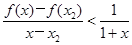 ,
,
由①②得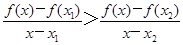 .
.
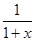 ,g′(x)=x2-x+b,x>-1,
,g′(x)=x2-x+b,x>-1,则
 解得
解得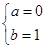
∴f(x)=ln(x+1)(x>-1),g(x)=
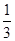 x3-
x3-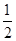 x2+x.
x2+x.令h(x)=f(x)-g(x)
=ln(x+1)-
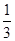 x3+
x3+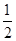 x2-x(x>-1),
x2-x(x>-1),∴h′(x)=
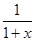 -x2+x-1=-
-x2+x-1=-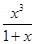 ,
,∴h(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
∴h(x)≤h(0)=0,∴f(x)≤g(x).
(2)当x∈(x1,x2)时,由题意得-1<x1<x<x2,
①设u(x)=(x+1)[f(x)-f(x1)]-(x-x1),
则u′(x)=ln(x+1)-ln(x1+1)>0,
∴u(x)>u(x1)=0,即(x+1)[f(x)-f(x1)]-(x-x1)>0,
∴
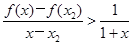 ;
;②设v(x)=(x+1)[f(x)-f(x2)]-(x-x2),
则v′(x)=ln(x+1)-ln(x2+1)<0,
∴v(x)>v(x2)=0,即(x+1)[f(x)-f(x2)]-(x-x2)>0,
∴
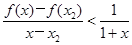 ,
,由①②得
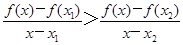 .
.
练习册系列答案
相关题目
 .
.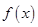 的极值;
的极值;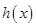 在区间
在区间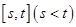 上的取值范围为
上的取值范围为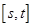 ,则称区间
,则称区间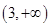 上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.
上是否存在“域同区间”?若存在,求出所有符合条件的“域同区间”;若不存在,请说明理由.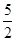 x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
x+b在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;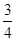 +
+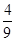 +…+
+…+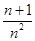 >ln(n+1)都成立.
>ln(n+1)都成立.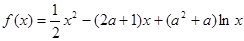 (
(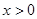 ,
,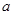 是常数),若对曲线
是常数),若对曲线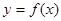 上任意一点
上任意一点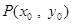 处的切线
处的切线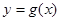 ,
,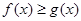 恒成立,求
恒成立,求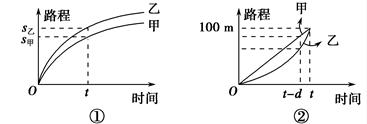
 x3-ax2-ax,g(x)=2x2+4x+c.
x3-ax2-ax,g(x)=2x2+4x+c.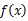 =
= 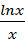 的最大值为( )
的最大值为( )