题目内容
2.用适当的符号填空.(1){a,b}?{a,b,c},a∈ {a,b,c};
(2)∅={x|x2+3=0},∅? R;
(3)N?{0,1},Q? N;
(4){0,1}={x|x2-x=0},2∈{x|x2-6x+8=0}
(5)√5-√2∈R,√16∈Z.
分析 根据子集、真子集、集合相等的概念,元素与集合关系的判断,以及自然数集、有理数集、以及实数集的关系及表示符号即可给每个空填上适当的符号.
解答 解:(1)a∈{a,b,c},b∈{a,b,c},且c∉{a,b};
∴{a,b}?{a,b,c};
a∈{a,b,c};
(2)方程x2+3=0无解,∴{x|x2+3=0}=∅;
即∅={x|x2+3=0},∅是任何非空集合的真子集;
∴∅?R;
(3)N是自然数的集合;
∴N?{0,1},Q是有理数的集合;
∴Q?N;
(4)解x2-x=0得,x=0,或1;
∴{0,1}={x|x2-x=0};
解x2-6x+8=0得,x=2,或4;
∴2∈{x|x2-6x+8=0};
(5)√5−√2∈R,√16=4;
∴√16∈Z.
故答案为:(1)?,∈,(2)=,?,(3)?,?,(4)=,∈,(5)∈,∈.
点评 考查子集、真子集、空集,以及集合相等的概念,元素与集合的关系,描述法、列举法表示集合,以及自然数集、有理数集、整数集,和实数集的表示符号.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
12.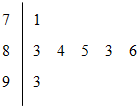 某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )
某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )
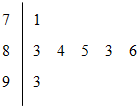 某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )
某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )| A. | 83,83 | B. | 83,83.5 | C. | 83,84 | D. | 84,83 |
10.设集合A={0,1,2,3,4},B={x∈R|x−4x−2≤0},则A∩B=( )
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {3,4} | D. | {x|2<x≤4} |
7.已知函数f(x)=3x3x+1,正项等比数列{an}满足a1008=1,则f(lna1)+f(lna2)+f(lna3)+…+f(lna2015)=( )
| A. | 2015 | B. | 20152 | C. | 2016 | D. | 1008 |