题目内容
7.已知函数$f(x)=\frac{3^x}{{{3^x}+1}}$,正项等比数列{an}满足a1008=1,则f(lna1)+f(lna2)+f(lna3)+…+f(lna2015)=( )| A. | 2015 | B. | $\frac{2015}{2}$ | C. | 2016 | D. | 1008 |
分析 由正项等比数列{an}的性质可得:ak•a2016-k=${a}_{1008}^{2}$=1,可得lnak+lna2016-k=0.又f(0)=$\frac{1}{2}$,f(x)+f(-x)=1,即可得出.
解答 解:由正项等比数列{an}的性质可得:ak•a2016-k=${a}_{1008}^{2}$=1,
∴lnak+lna2016-k=0.
f(0)=$\frac{1}{2}$,
又f(x)+f(-x)=$\frac{{3}^{x}}{{3}^{x}+1}$+$\frac{{3}^{-x}}{{3}^{-x}+1}$=$\frac{{3}^{x}}{{3}^{x}+1}$+$\frac{1}{{3}^{x}+1}$=1,
∴f(lna1)+f(lna2)+f(lna3)+…+f(lna2015)
=[f(lna1)+f(lna2015)]+[f(lna2)+f(lna2014)]+…+[f(lna1007)+f(a1009)]+f(lna1008)
=1007+$\frac{1}{2}$=$\frac{2015}{2}$.
故选:B.
点评 本题考查了等比数列的性质、函数的性质、对数的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知复数z满足(1-i)z=3+5i,则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.2${\;}^{1-\frac{1}{2}lo{g}_{2}3}$的值等于( )
| A. | $\frac{2}{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{2}{3}$$\sqrt{3}$ | D. | 2 |
17.点A,B,C,D在格点图的位置如图所示,则向量$\overrightarrow{AD}$+$\overrightarrow{AC}$在$\overrightarrow{AB}$方向上的投影为( )
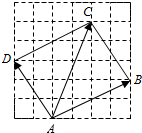

| A. | -$\frac{\sqrt{5}}{5}$ | B. | -$\frac{8\sqrt{5}}{5}$ | C. | $\frac{8\sqrt{5}}{5}$ | D. | 2 |
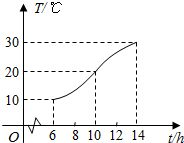 如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中$\frac{π}{2}<φ<π$),与图中曲线对应的函数解析式是$y=10sin(\frac{π}{8}x+\frac{3π}{4})+20,x∈[{6,14}]$.
如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中$\frac{π}{2}<φ<π$),与图中曲线对应的函数解析式是$y=10sin(\frac{π}{8}x+\frac{3π}{4})+20,x∈[{6,14}]$.