题目内容
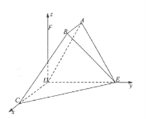
【题目】如下图,在空间多面体![]() 中,四边形
中,四边形![]() 为直角梯形,
为直角梯形,![]() ,
, ![]() ,
,![]() 是正三角形,
是正三角形,![]() ,
,![]() 。
。

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值。
的余弦值。
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() 。
。
【解析】
试题分析:(Ⅰ)借助题设条件运用面面垂直的判定定理推证;(Ⅱ)借助题设条件运用二面角的定义进行转化为平面角或运用空间向量的数量积公式求解。
试题解析:
证明:(Ⅰ)因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
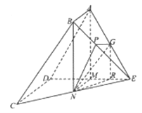
法一:(Ⅱ)取![]() 中点
中点![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() ,过
,过![]() 作
作![]() ,连接
,连接![]() ,所以
,所以![]() 是二面角
是二面角![]() 的平面角,
的平面角,
设![]() ,
,
在![]() 中,
中,![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,所以
,所以![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
在![]() 中,所以
中,所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
过![]() 作
作![]() ,则
,则![]() 是
是![]() 中点,
中点,
所以![]() ,
,
在![]() 中,
中,![]() ,
,
所以![]() ,即二面角
,即二面角![]() 的余弦值为
的余弦值为![]() 。
。
法二:(Ⅱ)过![]() 作
作![]() ,过
,过![]() 作
作![]() ,
,![]() ,
,
连接![]() ,则
,则![]() 是正方形,
是正方形,
因为![]() ,所以
,所以![]() ,
,
所以![]() 是梯形,
是梯形,
过![]() 作
作![]() ,连接
,连接![]() ,
,
因为![]() ,
,![]() 平面
平面![]() ,
,
所以![]() ,即
,即![]() ,
,
则![]() 是二面角
是二面角![]() 的平面角,
的平面角,
设![]() ,则
,则![]() ,
,
在![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,
所以二面角![]() 的余弦值为
的余弦值为![]() 。
。
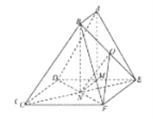
法三:(Ⅲ)过点![]() 作
作![]() 平面
平面![]() ,由(Ⅰ)知:平面
,由(Ⅰ)知:平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
以![]() 为原点,分别以
为原点,分别以![]() 为
为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,因为
,因为![]() ,且
,且![]() ,所以
,所以![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则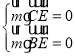 ,
,
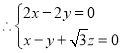 ,取
,取![]() ,
,
同理可得平面![]() 的法向量
的法向量![]() ,
,
所以![]() ,
,
因为二面角![]() 是钝角,所以其余弦值是
是钝角,所以其余弦值是![]() 。
。

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案【题目】某技术公司新开发了![]() 两种新产品,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种产品各100件进行检测,检测结果统计如下:
两种新产品,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种产品各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
产品 | 8 | 12 | 40 | 32 | 8 |
产品 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计产品![]() ,产品
,产品![]() 为正品的概率;
为正品的概率;
(2)生产一件产品![]() ,若是正品可盈利80元,次品则亏损10元;生产一件产品
,若是正品可盈利80元,次品则亏损10元;生产一件产品![]() ,若是正品可盈利100元,次品则亏损20元,在(1)的前提下,记
,若是正品可盈利100元,次品则亏损20元,在(1)的前提下,记![]() 为生产1件产品
为生产1件产品![]() 和1件产品
和1件产品![]() 所得的总利润,求随机变量
所得的总利润,求随机变量![]() 的分列和数学期望。
的分列和数学期望。
【题目】假设有两个分类变量X和Y的2×2列联表:
X\Y | y1 | y2 | 总计 |
x1 | a | 40 | a+40 |
x2 | 30﹣a | 30 | 60﹣a |
总计 | 30 | 70 | 100 |
在犯错误的概率不超过百分之5的前提下,下面哪个选项无法认为变量X,Y有关联( )
A.a=10
B.a=12
C.a=8
D.a=9
