Question

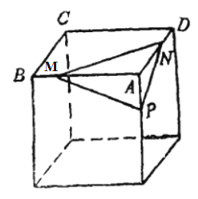
【题目】如图，设P、M、N分别是正方体的棱，AD，AB上非顶点的任意点.

①的外心必在的某一边上；

②的外心必在的内部；

③的垂心必是点A在平面PMN上的射影；

④若线段AP、AM、AN的长分别为a、b、c，则.其中（ ）.

A. 只有①、④正确.

B. 只有③、④正确.

C. 只有②、③、④正确.

D. 只有②、③正确.

Answer 1

【答案】C

【解析】

①设AM=a,AN=b,AP=c,所以，

在△PMN中，由余弦定理得，

所以∠PMN是锐角，同理∠PNM和∠MPN也是锐角，

所以△PMN是锐角三角形，所以的外心不在的某一边上.

所以① 是错误的.

②,的外心必在的内部，所以②是正确的.

③,由题得AN⊥平面ABP，设点A在底面PMN上的射影为O,则AO⊥平面PMN,

所以AO⊥PB,又因为PB⊥AN,所以PB⊥平面AON，所以PB⊥ON.

同理得PN⊥BO,所以点O是△PMN的垂心.所以③是正确的.

④,若线段AP、AM、AN的长分别为a、b、c，则,所以④是正确的.

故答案为：C