题目内容
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.
（1）根据散点图，直接判断甲、乙这五年年度体检的血压值谁的波动更大，并求波动更大者的方差；
（2）根据乙这五年年度体检血压值的数据，求年度体检血压值
关于年份
的线性回归方程，并据此估计乙在2018年年度体检的血压值.
（附：
，
）
【答案】（1）见解析；（2）见解析.
【解析】
（1）由图像可知，甲的波动更大，利用图像所给数据和方差的计算公式计算得方差的值.（2）将数据代入回归直线方程计算公式，计算出回归直线方程，并令
，求得
年度的预测值.
（1）甲的波动更大.
甲这五年年度体检的血压值的平均值为
,
其方差为
.
（2）∵
，
，
∴
，
.
故
关于
的线性回归方程为
.
当时，
，
故可估计乙在2018年年度体检的血压值为118.
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
【题目】大豆，古称菽，原产中国，在中国已有五千年栽培历史.2019年春，为响应中国大豆参与世界贸易的竞争，某市农科院积极研究，加大优良品种的培育工作，其中一项基础工作就是研究昼夜温差大小与大豆发芽率之间的关系.为此科研人员分别记录了7天中每天50粒大豆的发芽数得如下数据表格：
日期 | 4月3日 | 4月4日 | 4月5日 | 4月6日 | 4月7日 | 4月8日 | 4月9日 |
温差 | 8 | 9 | 10 | 12 | 11 | 8 | 13 |
发芽数 | 21 | 25 | 26 | 32 | 27 | 20 | 33 |
科研人员确定研究方案是：从7组数据中选5组数据求线性回归方程，再用求得的回归方程对剩下的2组数据进行检验.
（1）若选取的是4月4日至4月8日五天数据，据此求
关于
的线性回归方程
；
（2）若由线性回归方程得到的估计数据与实际数据的误差绝对值均不超过1粒，则认为得到的线性回归方程是可靠的，请检验（1）中回归方程是否可靠？
注：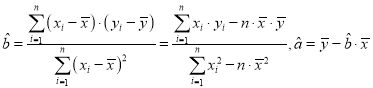
.
参考数值：
，
.
