题目内容
【题目】已知:在平面四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() (如图1),若将
(如图1),若将![]() 沿对角线BD折叠,使
沿对角线BD折叠,使![]() (如图2).请在图2中解答下列问题.
(如图2).请在图2中解答下列问题.
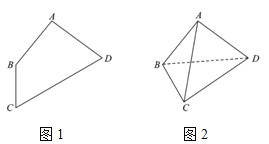
(1)证明:![]() ;
;
(2)求三棱锥![]() 的高.
的高.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)在图1中,根据平面几何知识可得BC=1且∠CBD=90°,在图2中可以得到AC2=AB2+CB2,从而可证明BC⊥平面ABD从而可证明结论.
(2)由(1)有![]() ,用等体积法有
,用等体积法有![]() .
.
证明:法1:由左图知,![]()
在△BDC中,∠CBD=135°-45°=90°,
∠BDC=75°-45°=30°,
![]() ,所以BC=1,
,所以BC=1,
又在右图中,因为AC![]() ,AB=AD
,AB=AD![]() ,所以AC2=AB2+CB2
,所以AC2=AB2+CB2
所以BC⊥AB
又因为∠CBD=90°,所以BC⊥平面ABD
所以BC⊥AD
法2:如右图,设BD的中点为O,连结A0,CO,因为∠A=90°,AB=AD![]()
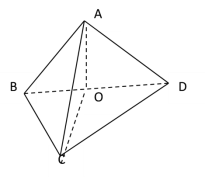
则![]()
由左图知,在△BDC中,∠CBD=135°-45°=90°
∠BDC=75°-45°=30°,所以BC=1,所以![]()
又因为AC![]() ,所以AC2=AO2+CO2
,所以AC2=AO2+CO2
所以AO⊥CO,所以AO⊥平面BCD,所以平面ABD⊥平面BCD,又∠CBD=90°
所以BC⊥平面ABD, 所以BC⊥AD
(2)因为AB=AD![]() ,AC
,AC![]() ,CD2=BC2+BD2=4
,CD2=BC2+BD2=4
所以CD2=AC2+AD2,所以AC⊥AD
设三棱锥B-ADC的高为h,则
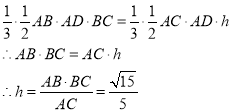

【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对200名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | ||
学习积极性不高 | 60 | ||
合计 | 200 |
已知在全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
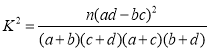 ,其中
,其中![]() .
.