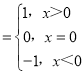题目内容
【题目】如图，已知在长方体
中，
，
，
，点
为
上的一个动点，平面
与棱
交于点
，给出下列命题：
①四棱锥
的体积为20；
②存在唯一的点，使截面四边形
的周长取得最小值
；
③当点不与
，
重合时，在棱
上均存在点
，使得
平面；
④存在唯一的点，使得
平面，且
．
其中正确的命题是_____（填写所有正确的序号）
【答案】①②③④
【解析】
由题意逐个讨论所给的命题，判断它们的真假．
解：①由题意可得
，
，所以①正确；
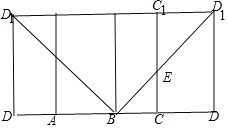
②将长方体展开，如图所示，恰好过
点时，截面的周长为
，
而在
中，
，所以最小值为
，
由面面平行的性质，可得四边形
为平行四边形，且
为展开图中唯一的点，所以②正确；
③点不与
，
重合，则
不会为
，即
不在面
内，
可作出的平面与平行，所以在棱
上均有相应的
，使得
面，故③正确；
④因为
，可得对角面
为正方形，可得
，
若
时，由三垂线定理可得
，即有
面，
矩形
中，，所以
，所以
，故④正确
综上可得：正确为①②③④.
故答案为：①②③④.
练习册系列答案
相关题目
