题目内容
11.已知数列{an}的前n项和Sn=2an+1,求证:{an}是等比数列,并求其通项公式.分析 由数列{an}的前n项和Sn,表示出Sn+1,根据Sn+1=Sn+an+1,整理得出an+1=2an,确定出{an}是公比为2的等比数列,求出首项即可确定出通项公式.
解答 证明:数列{an}的前n项和Sn=2an+1,
则有Sn+1=2an+1+1=Sn+an+1=2an+1+an+1,
整理得:an+1=2an,
当n=1时,S1=2a1+1=a1,即a1=-1,
则{an}是等比数列,其通项公式为an=-2n-1.
点评 此题考查了等比数列的确定,以及等比数列的通项公式,熟练掌握等比数列的性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.f(x)=($\frac{1}{2}$)x-x+1,用二分法求方程($\frac{1}{2}$)x-x+1=0在(0,3)内近似解的过程中,f(1)>0,f(1.5)<0,f(2)<0,f(3)<0,则方程的根落在区间( )
| A. | (1,1.5) | B. | (1.5,2) | C. | (2,3) | D. | 无法确定 |
2.cos(-30°)的值是( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
19.设复数z1=1-i,z2=-1+xi(x∈R),若z1z2为纯虚数,则x的值是( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
6.高二(6)班班主任对全班50名学生进行了有关作业量多少的调查,得到如下列联表:
认为“喜欢玩电脑游戏与认为作业多有关系”的概率有多大?
| 认为作业多 | 认为作业不多 | |
| 喜欢玩电脑游戏 | 18 | 9 |
| 不喜欢玩电脑游戏 | 8 | 15 |
1.函数y=$\sqrt{{(15+2x{-x}^{2})}^{3}}$的定义域是( )
| A. | {x|-3≤x≤5} | B. | {x|-3<x<5} | C. | {x|x≥5或x≤-3} | D. | R |
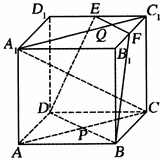 如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q,直线A1C与平面BDEF的交点为R.
如图:在正方体ABCD-A1B1C1D1中,E,F分别为D1C1,B1C1的中点,AC∩BD=P,A1C1∩EF=Q,直线A1C与平面BDEF的交点为R.