题目内容
16.已知向量$\overrightarrow{a}$=(sinθ,-2),$\overrightarrow{b}$=(1,cosθ),(0<θ<$\frac{π}{2}$),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,求sinθ和cosθ的值.分析 由已知可得sinθ=2cosθ,联立sin2θ+cos2θ=1,结合θ的范围求得sinθ和cosθ的值.
解答 解:$\overrightarrow{a}$=(sinθ,-2),$\overrightarrow{b}$=(1,cosθ),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\overrightarrow{a}•\overrightarrow{b}=sinθ-2cosθ=0$,
∴sinθ=2cosθ,
又sin2θ+cos2θ=1,
联立解得:$\left\{\begin{array}{l}{sinθ=\frac{2\sqrt{5}}{5}}\\{cosθ=\frac{\sqrt{5}}{5}}\end{array}\right.$或$\left\{\begin{array}{l}{sinθ=-\frac{2\sqrt{5}}{5}}\\{cosθ=-\frac{\sqrt{5}}{5}}\end{array}\right.$.
∵0<θ<$\frac{π}{2}$,
∴sinθ=$\frac{2\sqrt{5}}{5}$,cos$θ=\frac{\sqrt{5}}{5}$.
点评 本题考查平面向量的数量积运算,考查了三角函数的求值,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
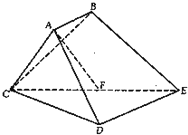 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.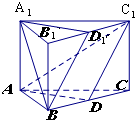 如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,求证:l1∥l2.
如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,求证:l1∥l2.