题目内容
6. 如图,AB和BC分别于圆O相切与点D,C,且AC经过圆心O,AC=2AD,求证:BC=2OD.
如图,AB和BC分别于圆O相切与点D,C,且AC经过圆心O,AC=2AD,求证:BC=2OD.
分析 先证明Rt△ADO∽Rt△ACB,可得$\frac{BC}{OD}=\frac{AC}{AD}$,利用AC=2AD,可得结论.
解答 证明:因为AB和BC分别与圆O相切于点D,C,所以∠ADO=∠ACB=90°
又因为∠A=∠A,所以Rt△ADO∽Rt△ACB,
所以$\frac{BC}{OD}=\frac{AC}{AD}$,
因为AC=2AD,
所以BC=2OD.
点评 本题考查圆的切线,考查三角形相似的判定与性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
17. 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )
 某几何体的三视图如图所示,则该几何体的表面积为( )
某几何体的三视图如图所示,则该几何体的表面积为( )| A. | 16 | B. | (10+$\sqrt{5}$)π | C. | 4+(5+$\sqrt{5})π$π | D. | 6+(5+$\sqrt{5})$π |
11.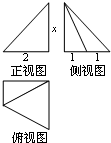 某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
 某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )| A. | 9 | B. | 8 | C. | 3 | D. | 6 |
 如图是一个几何体的三视图,根据图中数据,求该几何体的表面积和体积.
如图是一个几何体的三视图,根据图中数据,求该几何体的表面积和体积.