题目内容

17．某几何体的三视图如图所示，则该几何体的表面积为（　　）
A．16B．（10+$\sqrt{5}$）πC．4+（5+$\sqrt{5}）π$πD．6+（5+$\sqrt{5}）$π

分析 由该几何体的三视图判断出组合体各部分的几何特征，以及各部分的几何体相关几何量的数据，由面积公式求出该几何体的表面积．

解答 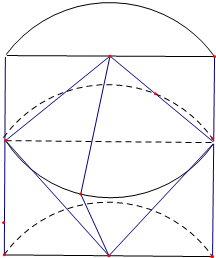解：由三视图可知其直观图如下，
半个圆柱的表面积为
π×1×（2+2）+π×12+2×2×1=5π+4，
两个半圆锥的表面积为
π×1×$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$π，
故表面积为4+（5+$\sqrt{5}$）π．
故选C．

点评 本题考查了由三视图求几何体的表面积，解题的关键是根据三视图判断几何体的结构特征及相关几何量的数据．

练习册系列答案
相关题目
7．已知F1，F2为椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左，右焦点，点P（1，$\frac{3}{2}$）在椭圆上，且|PF1|+|PF2|=4．
（Ⅰ）求椭圆E的方程；
（Ⅱ）过F1的直线l1，l2分别交椭圆E于A，C和B，D，且l1⊥l2，问是否存在常数λ，使得$\frac{1}{|AC|}$，λ，$\frac{1}{|BD|}$成等差数列？若存在，求出λ的值，若不存在，请说明理由．
8．已知$\frac{1}{3}≤k＜1$，设x1，x2（x1＜x2）是关于x的方程|2x-1|=k的两个实数根，x3，x4（x3＜x4）是方程|2x-1|=$\frac{k}{2k+1}$的两个实数根，则（x4-x3）+（x2-x1）的最小值是log23．
5．函数f（x）=sinωxcosφ-cosωxsinφ（ω＞0，0＜φ＜π）的图象过点（$\frac{π}{6}$，0），且相邻两条对称轴之间的距离为$\frac{π}{2}$
（1）（1）求f（x）的表达式；
（2）试求函数y=f2（$\frac{1}{2}x$）+$\frac{1}{2}$的单调增区间以及使得y$＞\frac{3}{4}$的x的取值范围．
12．已知数列{an}成等比数列，且an＜0，若a2-a1=8，a3=m．
（1）当m=48时，求数列{an}的通项公式；
（2）若数列{an}是唯一的，求m的值．
2．8人排成两排，每排4人，下列各有多少种不同的排法？
（1）甲、乙在前排两端，丙在后排左端；
（2）甲、乙在前排，丙在后排．
9．设e1、e2分别是具有公共焦点F1、F2的椭圆和双曲线的离心率，P是两曲线的一个公共点，O是F1F2的中点，且满足|PO|=|OF2|，则$\frac{{e}_{1}{e}_{2}}{\sqrt{{{e}_{1}}^{2}+{{e}_{2}}^{2}}}$=（　　）
A．$\frac{1}{3}$B．$\frac{1}{2}$C．$\frac{\sqrt{2}}{2}$D．$\sqrt{2}$
6．如图，AB和BC分别于圆O相切与点D，C，且AC经过圆心O，AC=2AD，求证：BC=2OD．
7．已知函数f（x）=$\frac{x}{{e}^{x}}$（x∈R），若x1≠x2，且f（x1）=f（x2），则x1，2-x2大小关系是大于．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网