题目内容
【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]
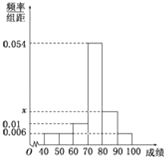
（Ⅰ）求图中
的值，并估计该班期中考试数学成绩的众数；
（Ⅱ）从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人，求这2人成绩均不低于90分的概率．
【答案】（Ⅰ）
，众数为75分；（Ⅱ）
.
【解析】
(Ⅰ)由题意利用小长方形面积之和为1可得x的值，由频率分布直方图的高度可得众数；
(Ⅱ)首先确定每组的人数，然后利用古典概型计算公式即可确定这2人成绩均不低于90分的概率.
（Ⅰ）由
，解得，
由频率分布直方图可知数学成绩的众数落在第四组，且众数为
75分．
（Ⅱ）分数在
的人数均为3人，共6人，
∴这2人成绩均不低于90分的概率
．
练习册系列答案
相关题目
【题目】二次函数图象上部分点的横坐标x，纵坐标y的对应值如下表：
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
（1）m= ；
（2）在图中画出这个二次函数的图象；
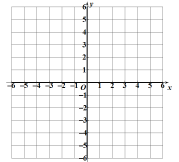
（3）当
时，x的取值范围是 ；
（4）当
时，y的取值范围是 ．
