Question

【题目】（10分）如图所示，在三棱锥中，底面，，，，动点D在线段AB 上．

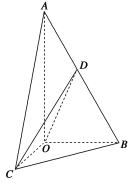
（1）求证：平面⊥平面；

（2）当时，求三棱锥的体积．

Answer 1

【答案】（1）证明详见解析；（2）．

【解析】

试题分析：本题主要考查线线垂直、线面垂直、面面垂直、锥体的体积等基础知识，考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力、计算能力．第一问，欲证平面⊥平面，根据面面垂直的判定定理可知在平面COD内一直线与平面AOB垂直，根据勾股定理可知，根据线面垂直的判定定理可知平面，而平面COD，满足定理所需条件；第二问，由第一问可知，所以面OBD为直角三角形，OC是锥体的高，利用锥体的体积公式计算体积即可得到结论．

试题解析：（1）证明：∵底面，

∴，．

∵，，

∴．又，

∴，

又

∴平面．

∵在平面内．

∴平面⊥平面．

解： ∵，

∴，．

∴．