题目内容
(本小题满分14分)已知直线 :y=k(x+2
:y=k(x+2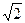 )与圆O:x2+y2=4相交于不重合的
)与圆O:x2+y2=4相交于不重合的
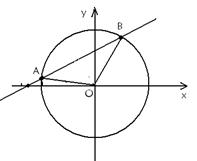
A、B两点,O是坐标原点,且三点A、B、O构成三角形.
(1)求k的取值范围;
(2)三角形ABO的面积为S,试将S表示成k的函数,并求出它的定义域;
(3)求S的最大值,并求取得最大值时k的值.
 :y=k(x+2
:y=k(x+2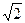 )与圆O:x2+y2=4相交于不重合的
)与圆O:x2+y2=4相交于不重合的A、B两点,O是坐标原点,且三点A、B、O构成三角形.
(1)求k的取值范围;
(2)三角形ABO的面积为S,试将S表示成k的函数,并求出它的定义域;
(3)求S的最大值,并求取得最大值时k的值.

解:(1)  ,而
,而 …4分
…4分
(2) …7分
…7分
 ,(
,( )…9分
)…9分
(3)设
 ,………12分
,………12分
 ,
,
∴S的最大值为2,取得最大值时 . ………14分
. ………14分
 ,而
,而 …4分
…4分(2)
 …7分
…7分 ,(
,( )…9分
)…9分(3)设

 ,………12分
,………12分 ,
, ∴S的最大值为2,取得最大值时
 . ………14分
. ………14分略

练习册系列答案
相关题目
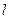 :x-y-1="0" 截得的弦长为2
:x-y-1="0" 截得的弦长为2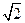 ,
,
 方程为
方程为  .
.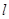 :y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则k的取值范围是
:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则k的取值范围是 ,-1)
,-1) 与圆
与圆 相交于
相交于 两点,若
两点,若 ,则
,则 的取值范围是( )
的取值范围是( )



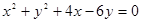 ,则其半径和圆心坐标分别为( )
,则其半径和圆心坐标分别为( ) 、(-2,3)
、(-2,3)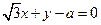 与圆
与圆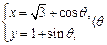 为参数)没有公共点,则a的取值范围是 .
为参数)没有公共点,则a的取值范围是 .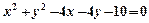 上恰有三个不同的点到直线
上恰有三个不同的点到直线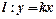 的距离为2
的距离为2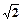 ,则
,则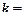 _____________________
_____________________