题目内容
（本小题满分12分）
已知一圆C的圆心为（2，-1），且该圆被直线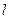
：x-y-1="0" 截得的弦长为2
，
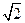（1）求该圆的方程
（2）求过弦的两端点的切线方程
（本小题满分12分）
已知一圆C的圆心为（2，-1），且该圆被直线
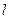：x-y-1="0" 截得的弦长为2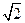，（1）求该圆的方程
（2）求过弦的两端点的切线方程
（本小题满分12分）
解：（1）设圆C的方程是
（r>0），则弦长P=2
，其中d为圆心到直线x-y-1=0
的距离，∴P=2
=2，∴
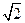，圆的方程为 
（2）由
，解得弦的二端点坐标是（2,1）、（0,-1），∴过弦二端点的该圆的切线方程是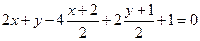
和
，即
和
（r>0），则弦长P=2，其中d为圆心到直线x-y-1=0的距离，∴P=2
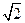=2，∴，圆的方程为 （2）由
，解得弦的二端点坐标是（2,1）、（0,-1），∴过弦二端点的该圆的切线方程是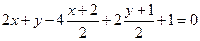和，即和略
练习册系列答案
相关题目
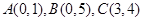三点，则以下选项中能与点
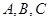在同一个圆上的点为（ ▲ ） 
的圆心坐标和半径分别为（ ）
A为边作正三角形PAB，且点B与圆心分别在PA的两侧，求四边形POAB面积的最大值．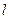
:y=k(x+2
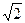)与圆O：x2+y2=4相交于不重合的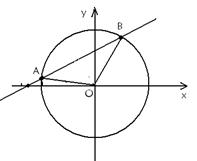
是圆
的直径，
、
是圆上的点，
，弧
和弧
的长相等，
是圆
，B、D是圆上两动点，且四边形ABCD是矩形（1）求顶点C的轨迹E的方程；
，C为
中点．点D，E分别在半径OA，OB上．若CD2＋CE2＋DE2＝
，则OD＋OE的取值范围是 ．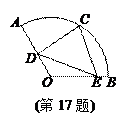
。
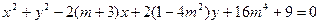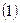、当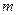
在什么范围内变化时，
该方程表示一个圆；
、当
变化时，求圆心的轨迹方程。