题目内容
直线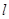 :y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则k的取值范围是
:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则k的取值范围是
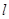 :y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则k的取值范围是
:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则k的取值范围是A.(- ,-1) ,-1) | B.(-1,1) | C.(-1,+ ) ) | D.(- ,-1)∪(-1,+ ,-1)∪(-1,+ ) ) |
D
分析:先将圆的方程化为标准方程,直线方程,化为一般方程.要使直线l:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则圆心到直线的距离小于半径,故可求k的取值范围.
解答:解:将圆化为标准方程:(x-1)2+(y-1)2=2,直线l:y=k(x-2)+2可化为:kx-y-2k+2=0
要使直线l:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则圆心到直线的距离小于半径
∴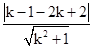 <
<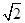
∴k2+2k+1>0
∴k≠-1
∴k的取值范围是(-∞,-1)∪(-1,+∞)
故选D.
解答:解:将圆化为标准方程:(x-1)2+(y-1)2=2,直线l:y=k(x-2)+2可化为:kx-y-2k+2=0
要使直线l:y=k(x-2)+2与圆x2+y2-2x-2y=0有两个不同的公共点,则圆心到直线的距离小于半径
∴
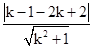 <
<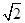
∴k2+2k+1>0
∴k≠-1
∴k的取值范围是(-∞,-1)∪(-1,+∞)
故选D.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 A为边作正三角形PAB,且点B与圆心分别在PA的两侧,求四边形POAB面积的最大值.
A为边作正三角形PAB,且点B与圆心分别在PA的两侧,求四边形POAB面积的最大值.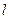 :y=k(x+2
:y=k(x+2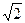 )与圆O:x2+y2=4相交于不重合的
)与圆O:x2+y2=4相交于不重合的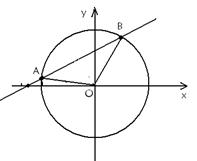
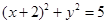 关于原点
关于原点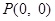 对称的圆的方程为( )
对称的圆的方程为( )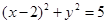 B
B 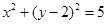
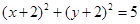 D
D 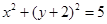
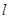 与圆
与圆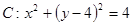 有公共点, 则直线
有公共点, 则直线
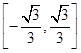
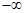 ,
,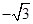 )∪[
)∪[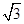 ,+
,+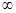 ]
]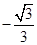 )∪[
)∪[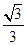 ,+
,+ 是圆
是圆 的直径,
的直径, 、
、 是圆上的点,
是圆上的点, ,弧
,弧 和弧
和弧 的长相等,
的长相等, 是圆
是圆





 ≤λ≤1
≤λ≤1  <
< ,C为
,C为 中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2=
中点.点D,E分别在半径OA,OB上.若CD2+CE2+DE2= ,则OD+OE的取值范围是 .
,则OD+OE的取值范围是 .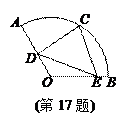
 过点
过点 且与圆
且与圆 相切,则
相切,则