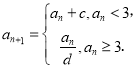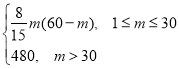题目内容
【题目】已知函数![]() -2为自然对数的底数,
-2为自然对数的底数,![]() ).
).
(1)若曲线![]() 在点
在点![]() 处的切线与曲线
处的切线与曲线![]() 至多有一个公共点时,求
至多有一个公共点时,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,若函数
时,若函数![]() 有两个零点,求
有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ![]() .
.
【解析】
(1)求导函数,确定曲线![]() 在点
在点![]() 处的切线,与
处的切线,与![]() 联立,利用根的判别式,即可得出结论;
联立,利用根的判别式,即可得出结论;
(2)由![]() 得
得![]() ,构造新函数,求导函数,确定其单调性,可得最值,即可确定
,构造新函数,求导函数,确定其单调性,可得最值,即可确定![]() 的取值范围.
的取值范围.
(1) ![]() ,所以切线斜率
,所以切线斜率![]()
又![]() ,∴曲线在点(1,0)处的切线方程为
,∴曲线在点(1,0)处的切线方程为![]()
由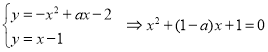 .
.
由![]() 可知:
可知:
当Δ=0时,即![]() 或
或![]() 时,有一个公共点;
时,有一个公共点;
当Δ<0时,即![]() 时,没有公共点.
时,没有公共点.
所以所求![]() 的取值范围为
的取值范围为![]() .
.
(2)![]() ,由
,由![]() ,得
,得![]() ,
,
令![]() ,则
,则![]() .
.
当x∈![]() 时,由
时,由![]() ,得
,得![]() .
.
所以![]() 在
在![]() 上单调递减,在[1,e]上单调递增,
上单调递减,在[1,e]上单调递增,
因此![]() ,由
,由![]() ,
,
比较可知![]() ,所以,结合函数图象可得,当
,所以,结合函数图象可得,当![]() 时,
时,
函数![]() 有两个零点.
有两个零点.
故所求![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目