题目内容
本小题满分14分)设函数 且
且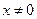 )
)
(1)求 的单调区间;
的单调区间;
(2)求 的取值范围;
的取值范围;
(3)已知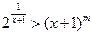 对任意
对任意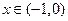 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
 且
且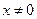 )
)(1)求
 的单调区间;
的单调区间;(2)求
 的取值范围;
的取值范围;(3)已知
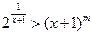 对任意
对任意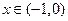 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。解:(1)
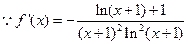 ………………………1分
………………………1分 当
当 时,即
时,即 ………………………2分
………………………2分当
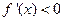 时,即
时,即
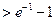 或
或 ………………………3分
………………………3分故函数
 的单调递增区间是
的单调递增区间是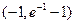 ………………………4分
………………………4分函数
 的单调递减区间是
的单调递减区间是 ………………………5分
………………………5分(2)由
 时,即
时,即 , ………………………6分
, ………………………6分由(1)可知
 在
在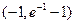 上递增, 在
上递增, 在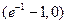 递减,所以在区间(-1,0)上,
递减,所以在区间(-1,0)上,当
 时,
时, 取得极大值,即最大值为
取得极大值,即最大值为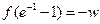 ………………………8分
………………………8分在区间
 上,
上, ………………………9分
………………………9分 函数
函数 的取值范围为
的取值范围为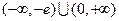 ………………………10分
………………………10分(3)
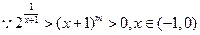 ,两边取自然对数得,
,两边取自然对数得,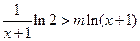 ………………………11分
………………………11分
略

练习册系列答案
相关题目
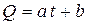 ;
;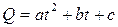 ;
;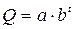 ;
;
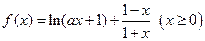
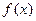 在
在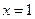 处取得极值,求实数
处取得极值,求实数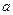 的值;
的值;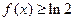 恒成立,求实数
恒成立,求实数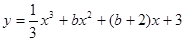 是R上的单调增函数,则
是R上的单调增函数,则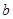 的取值范围是()
的取值范围是()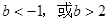
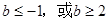
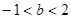
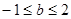
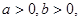 函数
函数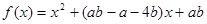 是偶函数,则
是偶函数,则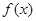 的图象与
的图象与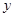 轴交点纵坐标的最小值为
轴交点纵坐标的最小值为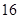
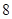
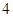
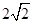
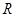 上的偶函数
上的偶函数 ,当
,当 时,
时,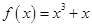 ,则当
,则当 时,
时,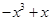
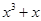
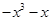

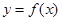 是定义在
是定义在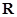 上的奇函数,
上的奇函数,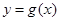 是定义在
是定义在 ,(其中
,(其中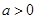 且
且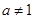 ),若
),若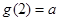 ,则
,则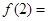 ( )
( )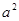
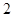
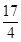
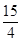
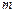 ,A、B相距100
,A、B相距100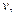 游泳速度为
游泳速度为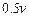 .
.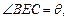 试将此人按上述路线从A到C所需时间T表示为
试将此人按上述路线从A到C所需时间T表示为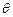 的函数,并求自变量
的函数,并求自变量
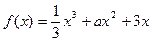 在(0,1)上不是单调函数,则实数a的取值范围为
在(0,1)上不是单调函数,则实数a的取值范围为