题目内容
已知函数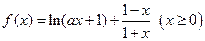
(1)若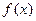 在
在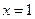 处取得极值,求实数
处取得极值,求实数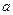 的值;
的值;
(2)若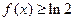 恒成立,求实数
恒成立,求实数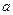 的取值范围.
的取值范围.
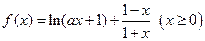
(1)若
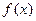 在
在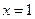 处取得极值,求实数
处取得极值,求实数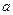 的值;
的值;(2)若
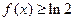 恒成立,求实数
恒成立,求实数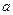 的取值范围.
的取值范围.(Ⅰ)
∵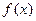 在
在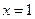 处取
处取 得极值,∴
得极值,∴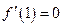 ,解得
,解得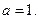
(Ⅱ)首先,由定义域知: 对于
对于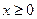 恒成立,可得
恒成立,可得 ;
;
由于:
①当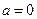 时,在
时,在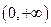 上,
上,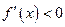 恒成立,所以,
恒成立,所以,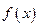 的单调递减区间为
的单调递减区间为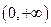 ;
;
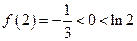 ,故此时
,故此时 不恒成立;
不恒成立; 
②当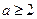 时,在区间
时,在区间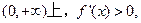 恒成立,所以,
恒成立,所以,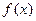 的单调增区间为
的单调增区间为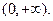 ,
, ,故此时恒成立;
,故此时恒成立;
③当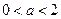 时,
时,
∴
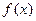 在
在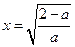 处取得最小值,只需
处取得最小值,只需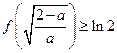 恒成立,
恒成立,
设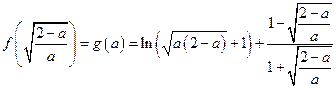
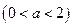 ,
,
设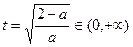 ,
,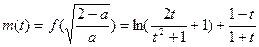
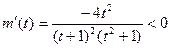 ,
,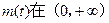 递减;又
递减;又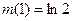
所以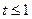 即
即 ,解得
,解得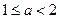
综上可知,若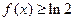 恒成立,只需
恒成立,只需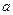 的取值范围是
的取值范围是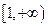

∵
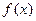 在
在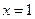 处取
处取 得极值,∴
得极值,∴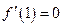 ,解得
,解得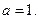
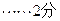
(Ⅱ)首先,由定义域知:
 对于
对于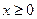 恒成立,可得
恒成立,可得 ;
; 由于:

①当
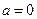 时,在
时,在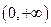 上,
上,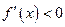 恒成立,所以,
恒成立,所以,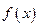 的单调递减区间为
的单调递减区间为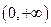 ;
;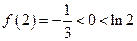 ,故此时
,故此时 不恒成立;
不恒成立; 
②当
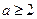 时,在区间
时,在区间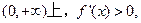 恒成立,所以,
恒成立,所以,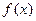 的单调增区间为
的单调增区间为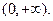 ,
, ,故此时恒成立;
,故此时恒成立;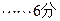
③当
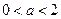 时,
时, |  |  | 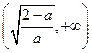 |
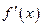 | - | 0 | + |
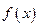 | ↘ | 极小值 | ↗ |

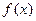 在
在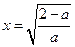 处取得最小值,只需
处取得最小值,只需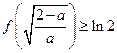 恒成立,
恒成立,设
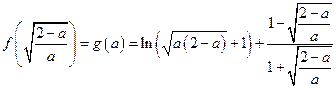
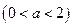 ,
,设
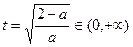 ,
,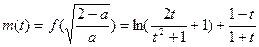
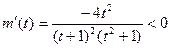 ,
,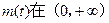 递减;又
递减;又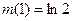
所以
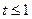 即
即 ,解得
,解得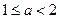
综上可知,若
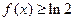 恒成立,只需
恒成立,只需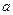 的取值范围是
的取值范围是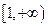
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 且
且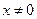 )
) 的单调区间;
的单调区间;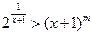 对任意
对任意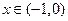 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。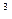 +3x
+3x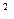 +ax+b)e
+ax+b)e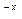 。
。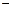 3 ,求f (x) 的单调区间;
3 ,求f (x) 的单调区间;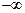 ,
,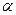 ),(2,
),(2,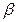 )上单调递增,在(
)上单调递增,在(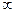 )上单调递减,证明:
)上单调递减,证明: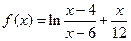
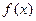 的单调区间以及极值;
的单调区间以及极值;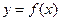 的图像是否为中心对称图形?如果是,请给出严格证明;如果不是,请说明理由。
的图像是否为中心对称图形?如果是,请给出严格证明;如果不是,请说明理由。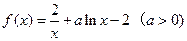 .
.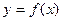 在点
在点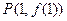 处的切线与直线
处的切线与直线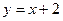 垂直,求函数
垂直,求函数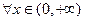 都有
都有 成立,试求
成立,试求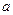 的取值范围;
的取值范围;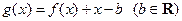 .当
.当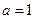 时,函数
时,函数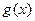 在区间
在区间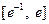 上有两个零点,
上有两个零点, 在点
在点 处的切线的斜率为( )
处的切线的斜率为( )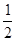
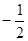
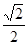

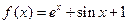 在
在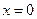 处的切线方程为
处的切线方程为