题目内容
【题目】已知椭圆E:![]() (
(![]() )的离心率为
)的离心率为![]() ,且短轴的一个端点B与两焦点A,C组成的三角形面积为
,且短轴的一个端点B与两焦点A,C组成的三角形面积为![]() .
.
(Ⅰ)求椭圆E的方程;
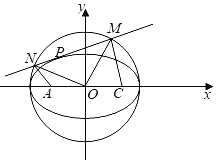
(Ⅱ)若点P为椭圆E上的一点,过点P作椭圆E的切线交圆O:![]() 于不同的两点M,N(其中M在N的右侧),求四边形
于不同的两点M,N(其中M在N的右侧),求四边形![]() 面积的最大值.
面积的最大值.
【答案】(Ⅰ)![]() ;(Ⅱ)4.
;(Ⅱ)4.
【解析】
(Ⅰ) 结合已知可得![]() ,
,![]() 求出a,b的值,即可得椭圆方程;
求出a,b的值,即可得椭圆方程;
(Ⅱ)由题意可知,直线的斜率存在,设出直线方程,联立直线方程与椭圆方程,利用判别式等于0可得![]() ,联立直线方程与圆的方程,结合根与系数的关系求得
,联立直线方程与圆的方程,结合根与系数的关系求得![]() ,利用弦长公式及点到直线的距离公式,求出
,利用弦长公式及点到直线的距离公式,求出![]() ,得到
,得到![]() ,整理后利用基本不等式求最值.
,整理后利用基本不等式求最值.
解:(Ⅰ)可得![]() ,
,![]() 结合
结合![]() ,
,
解得![]() ,
,![]() ,
,![]() ,得椭圆方程
,得椭圆方程![]() ;
;
(Ⅱ)易知直线![]() 的斜率k存在,设
的斜率k存在,设![]() :
:![]() ,
,
由![]() ,得
,得![]() ,
,
由![]() ,得
,得![]() ,
,
∵![]() ,
,
设点O到直线![]() :
:![]() 的距离为d,
的距离为d,
![]() ,
,![]()
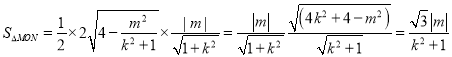 ,
,
由![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,
∴![]()
![]()
∴![]() ,
,
∴![]()
而![]() ,
,![]() ,易知
,易知![]() ,∴
,∴![]() ,则
,则![]() ,
,
四边形![]() 的面积
的面积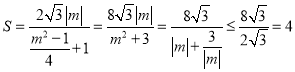
当且仅当![]() ,即
,即![]() 时取“
时取“![]() ”.
”.
∴四边形![]() 面积的最大值为4.
面积的最大值为4.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
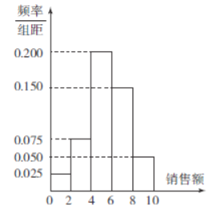
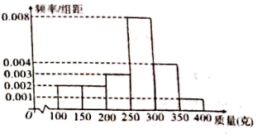
【题目】2019年10月1日,是中华人民共和国成立70周年纪念日.70年砥砺奋进,70年波澜壮阔,感染、激励着一代又一代华夏儿女,为祖国的繁荣昌盛努力拼搏,奋发图强.为进一步对学生进行爱国教育,某校社会实践活动小组,在老师的指导下,从学校随机抽取四个班级160名同学对这次国庆阅兵受到激励情况进行调查研究,记录的情况如下图:

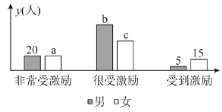
(1)如果从这160人中随机选取1人,此人非常受激励的概率和此人是很受激励的女同学的概率都是![]() ,求
,求![]() 的值;
的值;
(2)根据“非常受激励”与“很受激励”两种情况进行研究,判断是否有![]() 的把握认为受激励程度与性别有关.
的把握认为受激励程度与性别有关.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |