题目内容
已知数列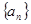 满足递推关系式
满足递推关系式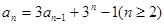 ,又
,又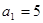 ,则使得
,则使得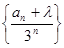 为等差数列的实数
为等差数列的实数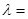 。
。
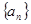 满足递推关系式
满足递推关系式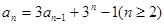 ,又
,又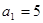 ,则使得
,则使得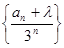 为等差数列的实数
为等差数列的实数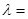 。
。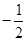
解:设bn=(an+λ)/ 3n,根据题意得bn为等差数列即2bn=bn-1+bn+1,而数列{an}满足递推式an=3an-1+3n-1(n≥2),
可取n=2,3,4得到(3a1+32-1+λ)/ 32 +(3a3+34-1+λ)/ 34 =2(3a2+33-1+λ) /33,
而a2=3a1+32-1,a3=3a2+33-1=3(3a1+32-1)=9a1+33-3,代入化简得λ="-1" /2 .
故答案为:-1/ 2
可取n=2,3,4得到(3a1+32-1+λ)/ 32 +(3a3+34-1+λ)/ 34 =2(3a2+33-1+λ) /33,
而a2=3a1+32-1,a3=3a2+33-1=3(3a1+32-1)=9a1+33-3,代入化简得λ="-1" /2 .
故答案为:-1/ 2

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
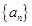 中,
中,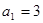 ,
,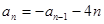 (
(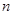 ≥2,且
≥2,且 ),数列
),数列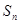 .
.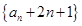 是等比数列,并求
是等比数列,并求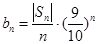 ,求
,求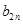 的最大值.
的最大值.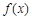 满足
满足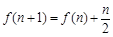 (n∈N *)且f (1) = 2,则f (20)为( )
(n∈N *)且f (1) = 2,则f (20)为( )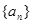 是等差数列,则数列
是等差数列,则数列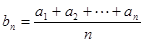 也为等差数列,类比上述性质,相应地:若数列
也为等差数列,类比上述性质,相应地:若数列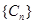 是等比数列,且
是等比数列,且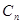 >0,则有
>0,则有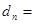 ▲ 也是等比数列.
▲ 也是等比数列.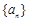 的前
的前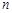 项和为
项和为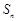 ,且
,且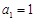 ,
,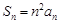
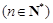 ,可归纳猜想出
,可归纳猜想出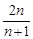
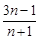
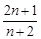

 满足
满足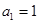 ,且
,且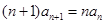 ,则数列
,则数列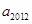 的值为( )
的值为( )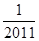
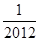
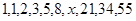 中,
中,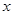 等于( )
等于( )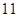
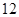
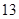
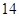
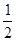 ,an+1=an+
,an+1=an+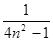 ,则an=________.
,则an=________.