题目内容
(本小题满分16分)
在数列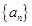 中,
中,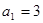 ,
,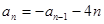 (
(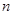 ≥2,且
≥2,且 ),数列
),数列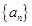 的前
的前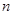 项和
项和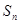 .
.
(1)证明:数列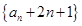 是等比数列,并求
是等比数列,并求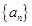 的通项公式;
的通项公式;
(2)求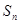 ;
;
(3)设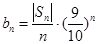 ,求
,求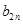 的最大值.
的最大值.
在数列
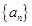 中,
中,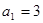 ,
,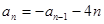 (
(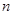 ≥2,且
≥2,且 ),数列
),数列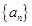 的前
的前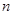 项和
项和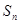 .
.(1)证明:数列
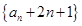 是等比数列,并求
是等比数列,并求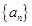 的通项公式;
的通项公式;(2)求
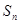 ;
;(3)设
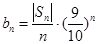 ,求
,求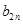 的最大值.
的最大值.(1)见解析;(2) ;(3)
;(3)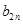 的最大值为
的最大值为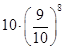 .
.
 ;(3)
;(3)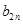 的最大值为
的最大值为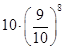 .
.第一问由题意,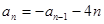 (
(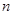 ≥2,且
≥2,且 ),
),
则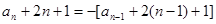 ,
,
又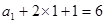 ,
,
∴数列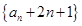 是首项为
是首项为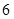 ,公比为
,公比为 的等比数列
的等比数列
第二问∵{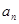 }的通项公式
}的通项公式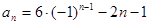 (
( ),
),
∴当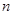 时偶数时,
时偶数时,
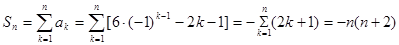 ,
,
当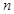 是奇数时,
是奇数时,
若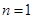 ,则
,则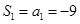
若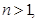 则
则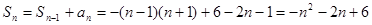
第三问(3)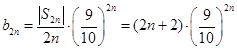 ,
, 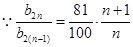 ,
,
令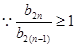 ,得
,得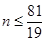 ,由于
,由于 ,
,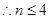 ,
,
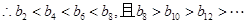
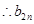 的最大值为
的最大值为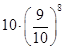
(1)证明:由题意,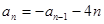 (
(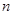 ≥2,且
≥2,且 ),
),
则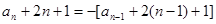 , ……………2分
, ……………2分
又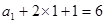 ,
,
∴数列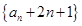 是首项为
是首项为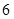 ,公比为
,公比为 的等比数列, ……………4分
的等比数列, ……………4分
∴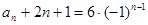 ,
,
∴{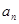 }的通项公式为
}的通项公式为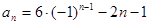 (
(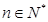 ); ……………6分
); ……………6分
(2)∵{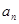 }的通项公式
}的通项公式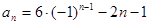 (
( ),
),
∴当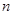 时偶数时,
时偶数时,
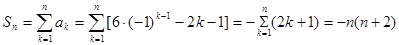 , ……………8分
, ……………8分
当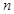 是奇数时,
是奇数时,
若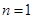 ,则
,则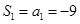
若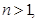 则
则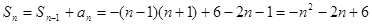 ,………10分
,………10分
综上: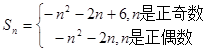 ; ……………11分
; ……………11分
(3)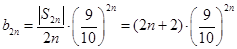 , ……………12分
, ……………12分
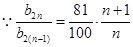 ,
,
令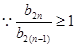 ,得
,得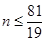 ,由于
,由于 ,
,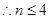 , ……………14分
, ……………14分
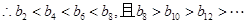
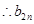 的最大值为
的最大值为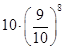 ……………16分
……………16分
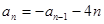 (
(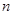 ≥2,且
≥2,且 ),
),则
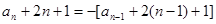 ,
, 又
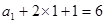 ,
,∴数列
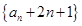 是首项为
是首项为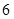 ,公比为
,公比为 的等比数列
的等比数列第二问∵{
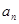 }的通项公式
}的通项公式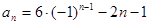 (
( ),
),∴当
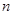 时偶数时,
时偶数时,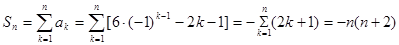 ,
,当
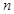 是奇数时,
是奇数时,若
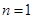 ,则
,则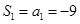
若
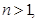 则
则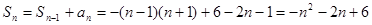
第三问(3)
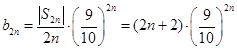 ,
, 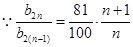 ,
,令
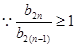 ,得
,得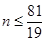 ,由于
,由于 ,
,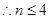 ,
, 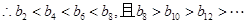
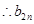 的最大值为
的最大值为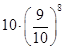
(1)证明:由题意,
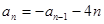 (
(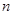 ≥2,且
≥2,且 ),
),则
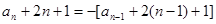 , ……………2分
, ……………2分又
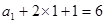 ,
,∴数列
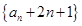 是首项为
是首项为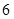 ,公比为
,公比为 的等比数列, ……………4分
的等比数列, ……………4分 ∴
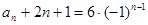 ,
,∴{
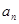 }的通项公式为
}的通项公式为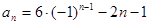 (
(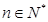 ); ……………6分
); ……………6分 (2)∵{
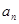 }的通项公式
}的通项公式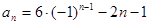 (
( ),
),∴当
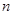 时偶数时,
时偶数时,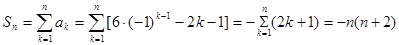 , ……………8分
, ……………8分当
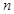 是奇数时,
是奇数时,若
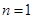 ,则
,则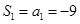
若
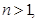 则
则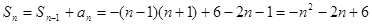 ,………10分
,………10分综上:
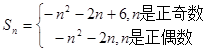 ; ……………11分
; ……………11分 (3)
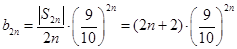 , ……………12分
, ……………12分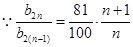 ,
,令
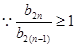 ,得
,得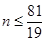 ,由于
,由于 ,
,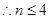 , ……………14分
, ……………14分 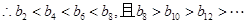
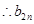 的最大值为
的最大值为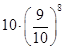 ……………16分
……………16分 
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
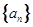 中,
中,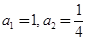 ,且
,且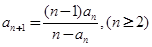 .
.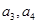 ,猜想
,猜想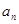 的表达式,并加以证明;
的表达式,并加以证明;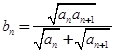 ,求证:对任意的自然数
,求证:对任意的自然数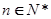 ,都有
,都有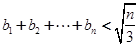 ;
;
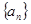 的前
的前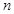 项和为
项和为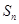 ,且
,且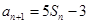
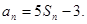 则
则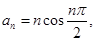 其前n项和为Sn,则S2012等于
其前n项和为Sn,则S2012等于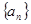 满足递推关系式
满足递推关系式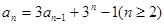 ,又
,又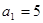 ,则使得
,则使得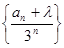 为等差数列的实数
为等差数列的实数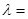 。
。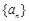 满足:
满足: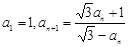 ,其前
,其前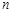 项和为
项和为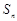 ,则
,则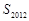 =( )
=( )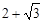
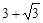
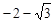
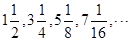 的前
的前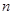 项和
项和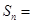 ▲ .
▲ .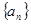 中,
中,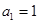 ,且对于任意
,且对于任意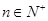 ,都有
,都有 ,则
,则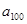 =
=