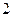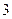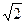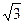题目内容
(12分)已知双曲线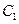 的渐近线方程是
的渐近线方程是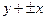 ,且它的一条准线与渐近线
,且它的一条准线与渐近线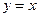 及
及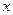 轴
轴
围成的三角形的周长是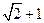
(I)求以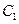 的两个顶点为焦点,以
的两个顶点为焦点,以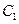 的焦点为顶点的椭圆
的焦点为顶点的椭圆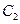 的方程;
的方程;
(II)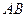 是椭圆
是椭圆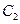 的长为
的长为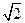 的动弦,
的动弦,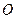 为坐标原来点,求
为坐标原来点,求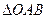 的面积
的面积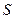 的取值范围。
的取值范围。
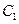 的渐近线方程是
的渐近线方程是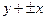 ,且它的一条准线与渐近线
,且它的一条准线与渐近线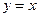 及
及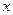 轴
轴围成的三角形的周长是
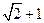
(I)求以
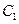 的两个顶点为焦点,以
的两个顶点为焦点,以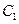 的焦点为顶点的椭圆
的焦点为顶点的椭圆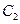 的方程;
的方程;(II)
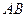 是椭圆
是椭圆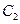 的长为
的长为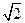 的动弦,
的动弦,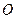 为坐标原来点,求
为坐标原来点,求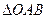 的面积
的面积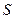 的取值范围。
的取值范围。(Ⅰ)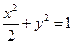 (Ⅱ)
(Ⅱ)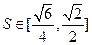
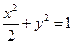 (Ⅱ)
(Ⅱ)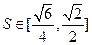
(I)由题意知双曲线焦点在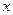 轴,设双曲线
轴,设双曲线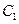 的方程为
的方程为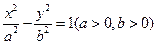
则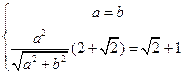 ,解得
,解得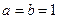
 双曲线
双曲线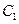 的方程为
的方程为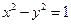 ,故椭圆
,故椭圆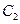 的方程为
的方程为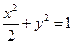
(II)(1)当直线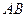 斜率不存在时,设直线
斜率不存在时,设直线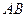 的方程为
的方程为 ,
,
则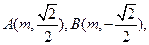 代入
代入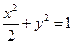 得
得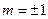 ,
,
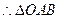 的面积
的面积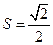
(2)当直线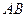 斜率存在时,设直线
斜率存在时,设直线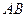 的方程为
的方程为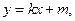 代入
代入
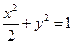
得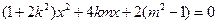
令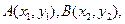 则
则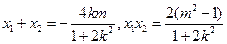
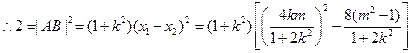
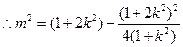
又原点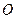 到
到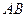 的距离为
的距离为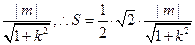
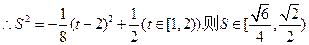
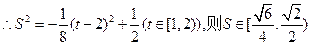
综合(1)(2)可知,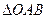 的面积
的面积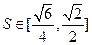
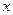 轴,设双曲线
轴,设双曲线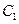 的方程为
的方程为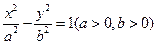
则
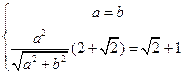 ,解得
,解得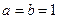
 双曲线
双曲线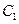 的方程为
的方程为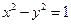 ,故椭圆
,故椭圆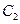 的方程为
的方程为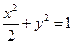
(II)(1)当直线
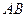 斜率不存在时,设直线
斜率不存在时,设直线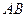 的方程为
的方程为 ,
,则
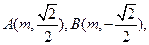 代入
代入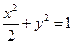 得
得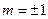 ,
,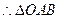 的面积
的面积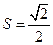
(2)当直线
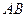 斜率存在时,设直线
斜率存在时,设直线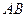 的方程为
的方程为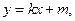 代入
代入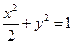
得
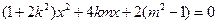
令
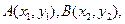 则
则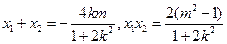
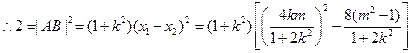
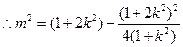
又原点
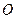 到
到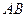 的距离为
的距离为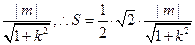
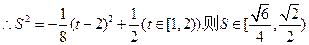
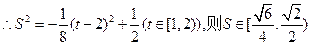
综合(1)(2)可知,
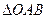 的面积
的面积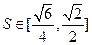

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
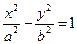 (a>0,b>0)的左、右焦点分别为F1、F2,过F1的直线与左支相交于A、B两点.如果|AF2|+|BF2|=2|AB|,那么|AB|=_________.
(a>0,b>0)的左、右焦点分别为F1、F2,过F1的直线与左支相交于A、B两点.如果|AF2|+|BF2|=2|AB|,那么|AB|=_________.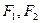 是双曲线
是双曲线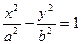 的左,右焦点,点
的左,右焦点,点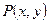 是双曲线右支上的一个动点,且
是双曲线右支上的一个动点,且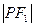 的最小值为
的最小值为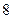 ,双曲线的一条渐近线方程为
,双曲线的一条渐近线方程为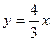 . 求双曲线的方程;
. 求双曲线的方程;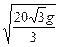 千米/秒,其中g为重力加速度,若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
千米/秒,其中g为重力加速度,若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?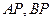 运送到
运送到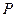 处,
处,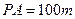 ,
,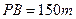 ,
, ,试说明怎样运才能最省工。
,试说明怎样运才能最省工。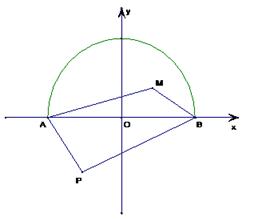
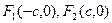 为双曲线
为双曲线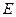 的两焦点,以
的两焦点,以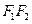 为直径的圆
为直径的圆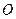 与双曲线
与双曲线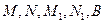 是圆
是圆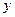 轴的交点,连接
轴的交点,连接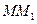 与
与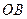 交于
交于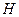 ,且
,且
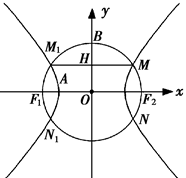
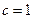 时,求双曲线
时,求双曲线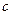 ,双曲线
,双曲线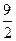 ,一个等比中项是
,一个等比中项是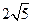 ,且
,且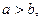 则双曲线
则双曲线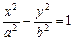 的离心率为( )
的离心率为( ) 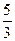
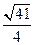
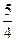
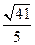
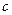 ,两条准线间的距离为
,两条准线间的距离为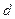 ,且
,且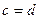 ,
,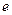 等于( )
等于( )