题目内容
舰A在舰B的正东6千米处,舰C在舰B的北偏西30°且与B相距4千米,它们准备捕海洋动物,某时刻A发现动物信号,4秒后B、C同时发现这种信号,A发射麻醉炮弹.设舰与动物均为静止的,动物信号的传播速度为1千米/秒,炮弹的速度是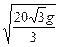 千米/秒,其中g为重力加速度,若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
千米/秒,其中g为重力加速度,若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
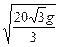 千米/秒,其中g为重力加速度,若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?
千米/秒,其中g为重力加速度,若不计空气阻力与舰高,问舰A发射炮弹的方位角和仰角应是多少?仰角θ=30°
取AB所在直线为x轴,以AB的中点为原点,建立如图所示的直角坐标系 由题意可知,A、B、C舰的坐标为(3,0)、(-3,0)、(-5,2
由题意可知,A、B、C舰的坐标为(3,0)、(-3,0)、(-5,2 ).
).
由于B、C同时发现动物信号,记动物所在位置为P,则|PB|=|PC|. 于是P在线段BC的中垂线上,易求得其方程为 x-3y+7
x-3y+7 =0.
=0.
又由A、B两舰发现动物信号的时间差为4秒,知|PB|-|PA|=4,故知P在双曲线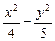 =1的右支上.
=1的右支上.
直线与双曲线的交点为(8,5 ),此即为动物P的位置,利用两点间距离公式,可得|PA|=10
),此即为动物P的位置,利用两点间距离公式,可得|PA|=10
据已知两点的斜率公式,得kPA= ,所以直线PA的倾斜角为60°,于是舰A发射炮弹的方位角应是北偏东30°.
,所以直线PA的倾斜角为60°,于是舰A发射炮弹的方位角应是北偏东30°.
设发射炮弹的仰角是θ,初速度v0=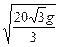 ,则
,则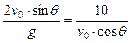 ,
,
∴sin2θ=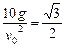 ,∴仰角θ=30°.
,∴仰角θ=30°.
 由题意可知,A、B、C舰的坐标为(3,0)、(-3,0)、(-5,2
由题意可知,A、B、C舰的坐标为(3,0)、(-3,0)、(-5,2 ).
).由于B、C同时发现动物信号,记动物所在位置为P,则|PB|=|PC|. 于是P在线段BC的中垂线上,易求得其方程为
 x-3y+7
x-3y+7 =0.
=0.又由A、B两舰发现动物信号的时间差为4秒,知|PB|-|PA|=4,故知P在双曲线
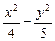 =1的右支上.
=1的右支上.直线与双曲线的交点为(8,5
 ),此即为动物P的位置,利用两点间距离公式,可得|PA|=10
),此即为动物P的位置,利用两点间距离公式,可得|PA|=10
据已知两点的斜率公式,得kPA=
 ,所以直线PA的倾斜角为60°,于是舰A发射炮弹的方位角应是北偏东30°.
,所以直线PA的倾斜角为60°,于是舰A发射炮弹的方位角应是北偏东30°.设发射炮弹的仰角是θ,初速度v0=
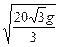 ,则
,则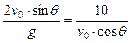 ,
,∴sin2θ=
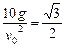 ,∴仰角θ=30°.
,∴仰角θ=30°.
练习册系列答案
相关题目
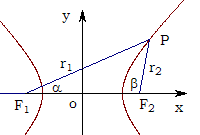
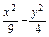 =1上的一点P与左、右两焦点F1、F2构成△PF1F2,求△PF1F2的内切圆与边F1F2的切点坐标.
=1上的一点P与左、右两焦点F1、F2构成△PF1F2,求△PF1F2的内切圆与边F1F2的切点坐标.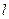 与离心率为
与离心率为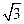 的双曲线
的双曲线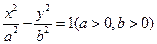 交于
交于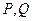 两点,
两点,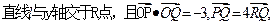 求直线与双曲线的方程
求直线与双曲线的方程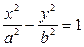 与
与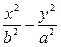 =1(a>b>0)的渐近线( )
=1(a>b>0)的渐近线( )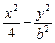 =1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.
=1(b∈N)的两个焦点F1、F2,P为双曲线上一点,|OP|<5,|PF1|,|F1F2|,|PF2|成等比数列,则b2=_________.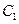 的渐近线方程是
的渐近线方程是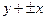 ,且它的一条准线与渐近线
,且它的一条准线与渐近线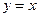 及
及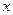 轴
轴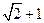
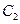 的方程;
的方程;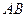 是椭圆
是椭圆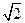 的动弦,
的动弦,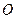 为坐标原来点,求
为坐标原来点,求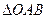 的面积
的面积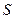 的取值范围。
的取值范围。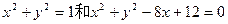
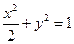 有相同的准线,且离心率为
有相同的准线,且离心率为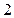 的双曲线的方程为( )
的双曲线的方程为( )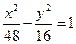
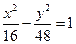
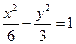
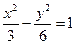
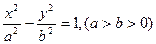 上异于顶点的任一点,双曲线的焦点为
上异于顶点的任一点,双曲线的焦点为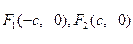 ,设
,设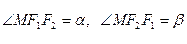 ,求
,求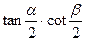 的值.
的值.