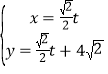题目内容
【题目】某石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探,由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用,勘探初期数据资料见如表:

(参考公式和计算结果:
 ,
, ![]() ,
, ![]() ,
, ![]() )
)
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() 的值,并估计
的值,并估计![]() 的预报值.
的预报值.
(2)现准备勘探新井![]() ,若通过1,3,5,7号并计算出的
,若通过1,3,5,7号并计算出的![]() ,
, ![]() 的值(
的值(![]() ,
, ![]() 精确到0.01)相比于(1)中的
精确到0.01)相比于(1)中的![]() ,
, ![]() ,值之差不超过10%,则使用位置最接近的已有旧井
,值之差不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(3)设出油量与勘探深度的比值![]() 不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数
不低于20的勘探井称为优质井,那么在原有6口井中任意勘探4口井,求勘探优质井数![]() 的分布列与数学期望.
的分布列与数学期望.
【答案】(1)![]() ,
, ![]() 的预报值为24;(2)使用位置最接近的已有旧井
的预报值为24;(2)使用位置最接近的已有旧井![]() ;(3)
;(3)![]() ,分布列见解析.
,分布列见解析.
【解析】试题分析:
(1)利用前5组数据与平均数的计算公式可得![]() =5,
=5,![]() =50,代入y=6.5x+a,可得a,进而定点y的预报值.
=50,代入y=6.5x+a,可得a,进而定点y的预报值.
(2)根据计算公式可得![]() ,
, ![]() ,
, ![]() ≈10.25,
≈10.25, ![]() =5.25,
=5.25, ![]() =10.25,计算可得并且判断出结论.
=10.25,计算可得并且判断出结论.
(3)由题意,1、3、5、6这4口井是优质井,2,4这两口井是非优质井,勘察优质井数X的可能取值为2,3,4,P(X=k)=![]() ,可得X的分布列及其数学期望.
,可得X的分布列及其数学期望.
解:
(1)因为![]() ,
, ![]() .
.
回归直线必过样本中心点![]() ,则
,则![]() .
.
故回归直线方程为![]() ,当
,当![]() 时,
时, ![]() ,即
,即![]() 的预报值为24.
的预报值为24.
(2)因为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
所以
![]() ,
,
![]() ,即
,即![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() ,
, ![]() ,均不超过10%,因此使用位置最接近的已有旧井
,均不超过10%,因此使用位置最接近的已有旧井![]() .
.
(3)由题意,1,3,5,6这4口井是优质井,2,4这两口井是非优质井,
所以勘察优质井数![]() 的可能取值为2,3,4,
的可能取值为2,3,4,
![]() ,
, ![]() ,
,
![]() .
.
X | 2 | 3 | 4 |
P |
|
|
|
![]()

【题目】为评估设备![]() 生产某种零件的性能,从设备
生产某种零件的性能,从设备![]() 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
直径/ | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
经计算,样本的平均值![]() ,标准差
,标准差![]() ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为![]() ,并根据以下不等式进行评判(
,并根据以下不等式进行评判(![]() 表示相应事件的概率);
表示相应事件的概率);
①![]() ;
;
②![]() ;
;
③![]()
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备![]() 的性能等级.
的性能等级.
(2)将直径小于等于![]() 或直径大于
或直径大于![]() 的零件认为是次品.
的零件认为是次品.
①从设备![]() 的生产流水线上随意抽取2件零件,计算其中次品个数
的生产流水线上随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() ;
;
②从样本中随意抽取2件零件,计算其中次品个数![]() 的数学期望
的数学期望![]() .
.
【题目】为了响应厦门市政府“低碳生活,绿色出行”的号召,思明区委文明办率先全市发起“少开一天车,呵护厦门蓝”绿色出行活动.“从今天开始,从我做起,力争每周至少一天不开车,上下班或公务活动带头选择步行、骑车或乘坐公交车,鼓励拼车……”铿锵有力的话语,传递了绿色出行、低碳生活的理念.
某机构随机调查了本市部分成年市民某月骑车次数,统计如下:
年龄 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
18岁至31岁 | 8 | 12 | 20 | 60 | 140 | 150 |
32岁至44岁 | 12 | 28 | 20 | 140 | 60 | 150 |
45岁至59岁 | 25 | 50 | 80 | 100 | 225 | 450 |
60岁及以上 | 25 | 10 | 10 | 18 | 5 | 2 |
联合国世界卫组织于2013年确定新的年龄分段:44岁及以下为青年人,45岁至59岁为中年人,60岁及以上为老年人.用样本估计总体的思想,解决如下问题:
(1)估计本市一个18岁以上青年人每月骑车的平均次数;
(2)若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()