题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 上存在两个极值点
上存在两个极值点![]() ,且
,且![]() ,证明:
,证明: ![]() .
.
【答案】(1) ![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】试题分析:(1)由条件可知![]() 恒成立,通过参变分离的方法得到
恒成立,通过参变分离的方法得到![]() 恒成立,即
恒成立,即![]() 转化为利用导数求函数
转化为利用导数求函数![]() 的最大值,即求
的最大值,即求![]() 的取值范围;(2)根据条件可知
的取值范围;(2)根据条件可知![]() ,
, ![]() 和
和![]() ,经过变形整理为
,经过变形整理为 ,经过换元,可将问题转化为证明
,经过换元,可将问题转化为证明![]() ,利用导数求函数的最小值,即可证明.
,利用导数求函数的最小值,即可证明.
试题解析:(1)由函数![]() 在
在![]() 上是减函数,知
上是减函数,知![]() 恒成立,
恒成立,
![]() .
.
由![]() 恒成立可知
恒成立可知![]() 恒成立,则
恒成立,则![]() ,
,
设![]() ,则
,则![]() ,
,
由![]() ,
, ![]() 知,
知,
函数![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,∴
上递减,∴![]() ,
,
∴![]() .
.
(2)由(1)知![]() .
.
由函数![]() 在
在![]() 上存在两个极值点
上存在两个极值点![]() ,且
,且![]() ,知
,知![]() ,
,
则![]() 且
且![]() ,
,
联立得![]() ,即
,即 ,
,
设![]() ,则
,则![]() ,
,
要证![]() ,
,
只需证![]() ,只需证
,只需证![]() ,只需证
,只需证![]() .
.
构造函数![]() ,则
,则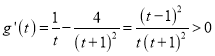 .
.
故![]() 在
在![]() 上递增,
上递增, ![]() ,即
,即![]() ,
,
所以![]() .
.

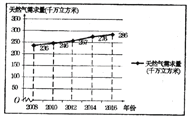
【题目】2017年12月,针对国内天然气供应紧张的问题,某市政府及时安排部署,加气站采取了紧急限气措施,全市居民打响了节约能源的攻坚战.某研究人员为了了解天然气的需求状况,对该地区某些年份天然气需求量进行了统计,并绘制了相应的折线图.
(Ⅰ)由折线图可以看出,可用线性回归模型拟合年度天然气需示量![]() (单位:千万立方米)与年份
(单位:千万立方米)与年份![]() (单位:年)之间的关系.并且已知
(单位:年)之间的关系.并且已知![]() 关于
关于![]() 的线性回归方程是
的线性回归方程是![]() ,试确定
,试确定![]() 的值,并预测2018年该地区的天然气需求量;
的值,并预测2018年该地区的天然气需求量;
(Ⅱ)政府部门为节约能源出台了《购置新能源汽车补贴方案》,该方案对新能源汽车的续航里程做出了严格规定,根据续航里程的不同,将补贴金额划分为三类,A类:每车补贴1万元,B类:每车补贴2.5万元,C类:每车补贴3.4万元.某出租车公司对该公司60辆新能源汽车的补贴情况进行了统计,结果如下表:
类型 |
|
|
|
车辆数目 | 10 | 20 | 30 |
为了制定更合理的补贴方案,政府部门决定利用分层抽样的方式了解出租车公司新能源汽车的补贴情况,在该出租车公司的60辆车中抽取6辆车作为样本,再从6辆车中抽取2辆车进一步跟踪调查.若抽取的2辆车享受的补贴金额之和记为“![]() ”,求
”,求![]() 的分布列及期望.
的分布列及期望.


