题目内容
15.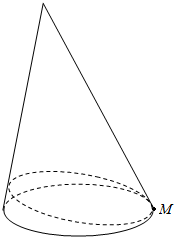 一个母线长为6的圆锥(如图)的底部圆周上有一昆虫(M点),如果它沿着圆锥的侧面爬行一周回到原来的位置的最短路程恰好为6,那么该圆锥的底面半径是多少?圆锥的高是多少?请求出该圆锥的侧面积与体积.(提示:平面上两点间的线段最短)
一个母线长为6的圆锥(如图)的底部圆周上有一昆虫(M点),如果它沿着圆锥的侧面爬行一周回到原来的位置的最短路程恰好为6,那么该圆锥的底面半径是多少?圆锥的高是多少?请求出该圆锥的侧面积与体积.(提示:平面上两点间的线段最短)
分析 把圆锥侧面展开成一个扇形,则对应的弧长是底面的周长,对应的弦是最短距离,得出底面半径、高,即可求出该圆锥的侧面积与体积.
解答 解:把圆锥侧面展开成一个扇形,则对应的弧长是底面的周长,对应的弦是最短距离.
∵母线长为6,沿着圆锥的侧面爬行一周回到原来的位置的最短路程恰好为6,
∴侧面展开图的圆心角是60°,
设底面半径为r,则2πr=$\frac{π}{3}×6$,
解得:r=1,
∴圆锥的高是$\sqrt{36-1}$=$\sqrt{35}$,
∴圆锥的侧面积为$π•{1}^{2}+\frac{1}{2}•2π•1•6$=7π,体积V=$\frac{1}{3}•π•{1}^{2}•\sqrt{35}$=$\frac{\sqrt{35}π}{3}$.
点评 本题考查了平面展开-最短路线问题,弧长公式,圆锥的侧面积与体积,关键是能求出底面半径、高.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
6.a,b,c为三个人,命题P:“如果b的年龄不是最大的,那么a的年龄最小”和命题Q:“如果c的年龄不是最小的,那么a的年龄最大”都是真命题,则a,b,c的年龄大小顺序是( )
| A. | b>a>c | B. | a>c>b | C. | c>b>a | D. | 不能确定 |
4.等差数列{an}、{bn}中的前n项和分别为Sn、Tn,$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n}{3n+1}$,则$\frac{{a}_{10}}{{b}_{10}}$=( )
| A. | $\frac{20}{31}$ | B. | $\frac{19}{29}$ | C. | $\frac{17}{28}$ | D. | $\frac{16}{27}$ |
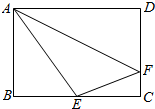 在矩形ABCD中,已知$AB=\sqrt{3},AD=2$,点E是BC的中点,点F在CD上,若$\overrightarrow{AB}•\overrightarrow{AF}$=$\sqrt{3}$,则$\overrightarrow{AE}•\overrightarrow{BF}$的值是$\sqrt{3}$-1.
在矩形ABCD中,已知$AB=\sqrt{3},AD=2$,点E是BC的中点,点F在CD上,若$\overrightarrow{AB}•\overrightarrow{AF}$=$\sqrt{3}$,则$\overrightarrow{AE}•\overrightarrow{BF}$的值是$\sqrt{3}$-1.