题目内容
5.已知${log_a}\frac{1}{2}<1$,则a∈$(0,\frac{1}{2})∪(1,+∞)$.分析 把不等式两边化为同底数,然后分类利用对数函数的性质求得a的范围.
解答 解:由${log_a}\frac{1}{2}<1$=logaa,
当a>1时,不等式成立;
当0<a<1时,得0$<a<\frac{1}{2}$.
∴${log_a}\frac{1}{2}<1$的解集为$(0,\frac{1}{2})∪(1,+∪)$.
故答案为:$(0,\frac{1}{2})∪(1,+∪)$.
点评 本题考查对数不等式的解法,考查了分类讨论的数学思想方法,是基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
20.下列等式成立的是( )
| A. | log2[(-3)(-5)]=log2(-3)+log2(-5) | B. | log2(-10)2=2log2(-10) | ||
| C. | log2[(-3)(-5)]=log23+log25 | D. | log2(-5)3=-log253 |
14.已知函数$f(x)=\left\{\begin{array}{l}m{x^2}-8ax+n,x<1\\ log_a^x\begin{array}{l}{\begin{array}{l},{x≥1}\end{array}}\end{array}\end{array}\right.$,其中m为函数$g(x)=2x+\sqrt{x-1}$的最小值,n为函数$h(x)={3^{1-{x^2}}}$的最大值,且对任意x1≠x2,都有$\frac{{f({x_2})-f({x_1})}}{{{x_1}-{x_2}}}>0$成立,则实数a的取值范围是( )
| A. | $(0,\frac{1}{2}]$ | B. | (1,2] | C. | $[\frac{5}{8},1)$ | D. | $[\frac{1}{2},\frac{5}{8}]$ |
15.已知圆锥的高为8,底面圆的直径为12,则此圆锥的侧面积是( )
| A. | 24π | B. | 30π | C. | 48π | D. | 60π |
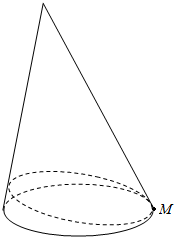 一个母线长为6的圆锥(如图)的底部圆周上有一昆虫(M点),如果它沿着圆锥的侧面爬行一周回到原来的位置的最短路程恰好为6,那么该圆锥的底面半径是多少?圆锥的高是多少?请求出该圆锥的侧面积与体积.(提示:平面上两点间的线段最短)
一个母线长为6的圆锥(如图)的底部圆周上有一昆虫(M点),如果它沿着圆锥的侧面爬行一周回到原来的位置的最短路程恰好为6,那么该圆锥的底面半径是多少?圆锥的高是多少?请求出该圆锥的侧面积与体积.(提示:平面上两点间的线段最短)