题目内容
10.已知函数f(x)=sinωx(ω>0).(1)当ω=2时,写出由y=f(x)的图象向右平移$\frac{π}{6}$个单位长度得到的图象所对应的函数解析式;
(2)若y=f(x)图象过点$(\frac{2π}{3},0)$,且在区间$(0,\frac{π}{3})$上是增函数,求ω的值.
分析 (1)根据函数图象的平移得出答案
(2)利用零点得出$\frac{2π}{3}$ω=kπ,即ω=$\frac{3k}{2}$,k∈z,再根据单调性得出$\frac{π}{3}$ω$≤\frac{π}{2}$,即ω≤$\frac{3}{2}$,判断得出ω的值.
解答 解:(1)∵函数f(x)=sinωx(ω>0).
ω=2时,f(x)=sin2x.
∴图象向右平移$\frac{π}{6}$个单位长度得到:y=sin2(x-$\frac{π}{6}$).
(2)∵函数f(x)=sinωx(ω>0).
图象过点$(\frac{2π}{3},0)$,
∴$\frac{2π}{3}$ω=kπ,即ω=$\frac{3k}{2}$,k∈z,
∵函数f(x)=sinωx(ω>0).在区间$(0,\frac{π}{3})$上是增函数,
得出:$\frac{π}{3}$ω$≤\frac{π}{2}$,即ω≤$\frac{3}{2}$,
∵ω>0,∴$ω=\frac{3}{2}$
点评 本题综合考察了三角函数的图象和性质,转化化思想,方程的利用,属于中档题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
20.下列等式成立的是( )
| A. | log2[(-3)(-5)]=log2(-3)+log2(-5) | B. | log2(-10)2=2log2(-10) | ||
| C. | log2[(-3)(-5)]=log23+log25 | D. | log2(-5)3=-log253 |
 已知函数f(x)=logax(a>0,a≠1)
已知函数f(x)=logax(a>0,a≠1)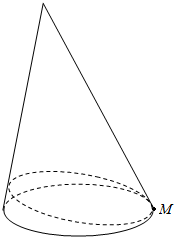 一个母线长为6的圆锥(如图)的底部圆周上有一昆虫(M点),如果它沿着圆锥的侧面爬行一周回到原来的位置的最短路程恰好为6,那么该圆锥的底面半径是多少?圆锥的高是多少?请求出该圆锥的侧面积与体积.(提示:平面上两点间的线段最短)
一个母线长为6的圆锥(如图)的底部圆周上有一昆虫(M点),如果它沿着圆锥的侧面爬行一周回到原来的位置的最短路程恰好为6,那么该圆锥的底面半径是多少?圆锥的高是多少?请求出该圆锥的侧面积与体积.(提示:平面上两点间的线段最短)