题目内容
【题目】已知函数f(x)=ex﹣ax+a(a∈R),其中e为自然对数的底数.
(1)讨论函数y=f(x)的单调性;
(2)函数y=f(x)的图象与x轴交于A(x1 , 0),B(x2 , 0)两点,x1<x2 , 点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记 ![]() ,求at﹣(a+t)的值.
,求at﹣(a+t)的值.
【答案】
(1)解:函数f(x)=ex﹣ax+a,f'(x)=ex﹣a,
①当a≤0时,则f'(x)>0,则函数f(x)在(﹣∞,+∞)是单调增函数.
②当a>0时,令f'(x)=0,则x=lna,
若x<lna,f'(x)<0,所以f(x)在(﹣∞,lna)上是单调减函数;
若x>lna,f'(x)>0,所以f(x)在(lna,+∞)上是单调增函数.
(2)解:由(1)可知当a>0时,函数y=f(x)其图象与x轴交于两点,则有 ![]() ,则
,则 ![]() ,则xi>1(i=1,2).
,则xi>1(i=1,2).
于是 ![]() ,在等腰三角形ABC中,显然C=90°,所以
,在等腰三角形ABC中,显然C=90°,所以 ![]() ,即y0=f(x0)<0,
,即y0=f(x0)<0,
由直角三角形斜边的中线性质,可知 ![]() ,
,
所以 ![]() ,即
,即 ![]() ,
,
所以 ![]() ,
,
即 ![]() .
.
因为x1﹣1≠0,则 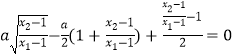 ,
,
又 ![]() ,所以
,所以 ![]() ,
,
即 ![]() ,则(a﹣1)(t﹣1)=2.
,则(a﹣1)(t﹣1)=2.
所以at﹣(a+t)=1.
【解析】(1)求导,分类讨论,根据导数与函数单调性的关系,即可求得f(x)的单调性区间;(2)由题意可知:C=90°,则 ![]() ,即y0=f(x0)<0,然后得到关于参数a的方程
,即y0=f(x0)<0,然后得到关于参数a的方程 ![]() ,则
,则 ![]() ,则(a﹣1)(t﹣1)=2.即可求得at﹣(a+t)=1.
,则(a﹣1)(t﹣1)=2.即可求得at﹣(a+t)=1.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】棉花的纤维长度是评价棉花质量的重要指标,某农科所的专家在土壤环境不同的甲、乙两块实验地分别种植某品种的棉花,为了评价该品种的棉花质量,在棉花成熟后,分别从甲、乙两地的棉花中各随机抽取20根棉花纤维进行统计,结果如下表:(记纤维长度不低于300mm的为“长纤维”,其余为“短纤维”)
纤维长度 | (0,100) | [100,200) | [200,300) | [300,400) | [400,500] |
甲地(根数) | 3 | 4 | 4 | 5 | 4 |
乙地(根数) | 1 | 1 | 2 | 10 | 6 |
(1)由以上统计数据,填写下面2×2列联表,并判断能否在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.
甲地 | 乙地 | 总计 | |
长纤维 | |||
短纤维 | |||
总计 |
附:(1) ![]() ;(2)临界值表;
;(2)临界值表;
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)现从上述40根纤维中,按纤维长度是否为“长纤维”还是“短纤维”采用分层抽样的方法抽取8根进行检测,在这8根纤维中,记乙地“短纤维”的根数为X,求X的分布列及数学期望.


